Radioss Coordinate System
- Global system (, , and )
- Natural system (isoparametric frame) ()
- Local element coordinate system (, , and )
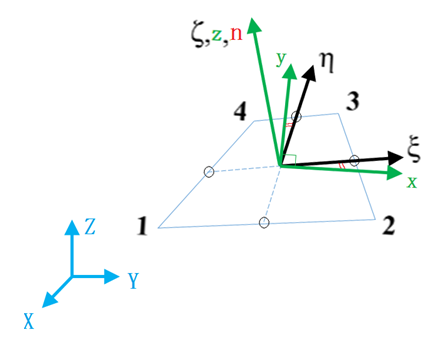
Figure 1. 4-Node Shell Element
(, , and ) - Global Cartesian fixed system:
() - Natural system (non-normalized coordinate system).
- is from middle point of Line 14 to middle point of Line 23.
- is from middle point of Line 12 to middle point of Line 34.
- Plane () is in the middle surface of shell element and is normal of the middle surface.
- is normal of middle surface.
- ( and ) are in the middle surface
- and are positioned so that they have same angle between and , and
The origin of () and (, , and ) are the same as it is at the intersection point of middle point line.
3-node Shell Element
(, , and ) - Global Cartesian fixed system
() - Natural system (non-normalized coordinate system).
- is from Node 1 to Node 2.
- is from Node 1 to Node 3.
- Plane () is in the middle surface of shell element and is normal of the middle surface.
- is normal of middle surface.
- is from Node 1 to Node 2.
- is orthogonal to and ( and ) are in the middle surface.
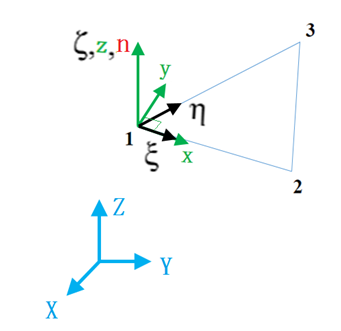
Figure 2.
Solids and Thick Shells (hexa)
- Global system (, , and )
- Natural system (, , and )
- Local element coordinate system (, , and )
- Material system
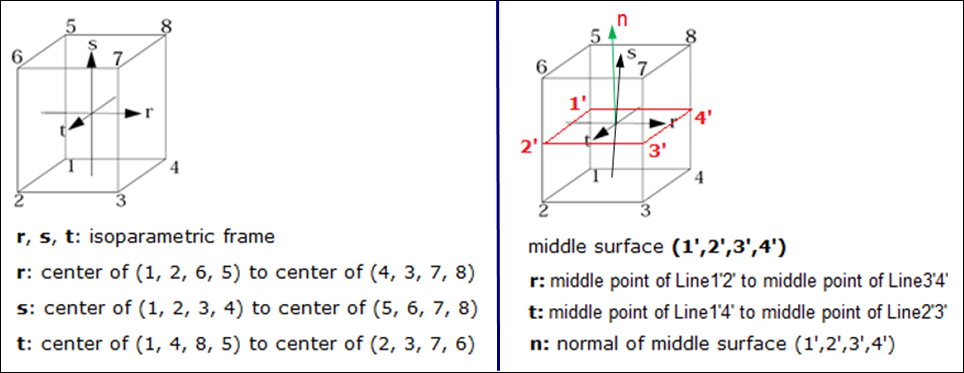
Figure 3. Solids and Thick Shells (hexa)
(, , and ) - Global Cartesian fixed system
- is from the center of surface (1, 2, 6, and 5) to center of surface (4, 3, 7, and 8)
- is from the center of surface (1, 2, 3, and 4) to center of surface (5, 6, 7, and 8)
- is from the center of surface (1, 4, 8, and 5) to center of surface (2, 3, 7, and 6)
- is also from middle point of Line 1' and 2' to middle point of Line 3' and 4'.
- is also from middle point of Line 1' and 2' to middle point of Line 3' and 4'
- is normal of middle surface (1', 2', 3', and 4')
(, , and ) - Local coordinate system (orthogonal, normalized elemental coordinate system).
Local coordinate system in middle surface (1', 2', 3', and 4') is the same as the local coordinate system in middle surface (1, 2, 3, and 4) for shell element. r in solid is the same as in shell element.
Tetra Elements
- is from node 4 to node 1
- is from node 4 to node 2
- is from node 4 to node 3
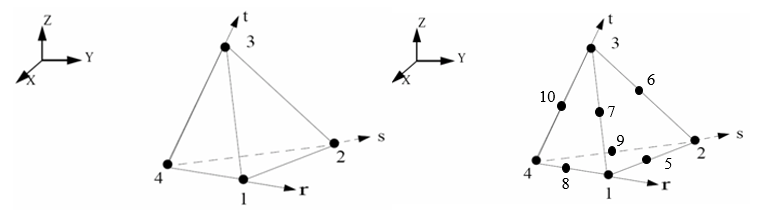
Figure 4. Tetra Elements
Material System
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| VX | VY | VZ | |||||||
Use vector and angle material direction 1 () can be defined (along normal n project vector to middle surface and get vector . Rotate angle of vector then get material direction . Material direction is normally the fiber direction. For composite, a different ply could be defined with one vector and different .
- is normal of shell middle surface
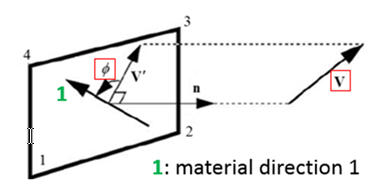
Figure 5.
- Iorth=0 (default): The orthotropic direction follows the local co-rotational reference. The angle between and is constant during the simulation. Internal force is computed in local frame and then rotated to the global system. This formulation is more accurate, if a large rotation occurs.
- Iorth=1: The orthotropic direction is attached to the
local isoparametric frame. The angle between and is updated during the simulation. It is
updated in a way that projection of vector to and is always constant during the simulation.
Pure shear could not well descripted with this method, but traction could
well be described. So, this method usually is used to defined fiber
direction in airbag.
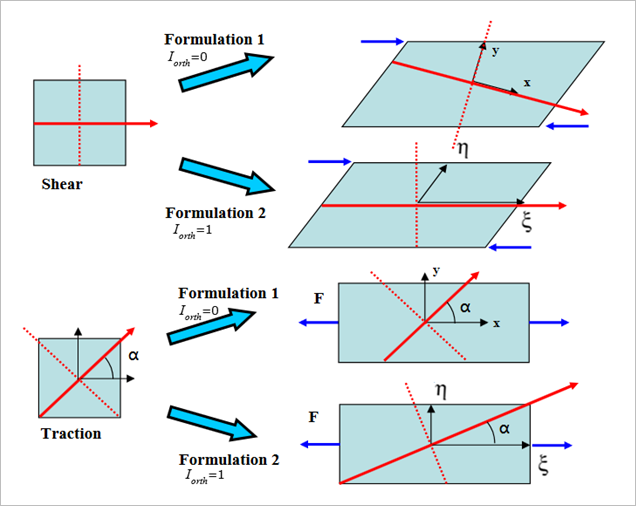
Figure 6.
- IP=0
- Use Skew_ID
- IP=1
- Plane (,) + angle
- IP=2
- Plane (,) + angle
- IP=3
- Plane (,) + angle
- IP=11
- Plane (,) + orthogonal projection of references vector on plane (,)
- IP=12
- Plane (,) + orthogonal projection of references vector on plane (,)
- IP=13
- Plane (,) + orthogonal projection of references vector on plane (,)
- Definition is the same for any Isolid and Iframe parameters
- In the simplest case, material directions , and directly with skew (IP=0) are recommended
- For IP > 0 the isoparametric, non-orthogonal system , , and , is used to determine material
directions.
- First material axis is determined according to IP.
- For example, for IP=1
- The first material axis and is orthogonal and rotated by angle in the ( and ) plane.
- The third material axis is normal of and plane (vector product of and ).
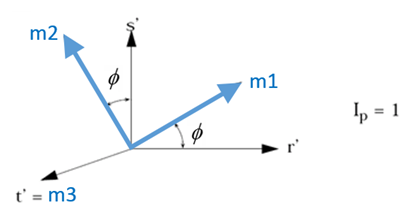
Figure 7. - The (, , and ) system is orthogonal and it is
generated from non-orthogonal isoparametric system (, , and ).
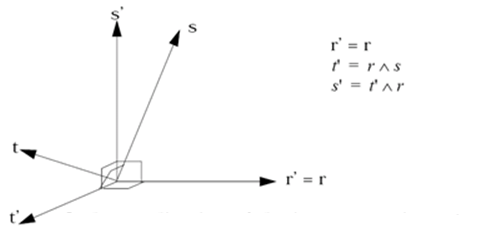
Figure 8. Orthogonalization of the Isoparametric System
Depending on Isolid and Iframe parameters, three definitions of systems are used in Radioss for hexa elements (8-noded bricks) using /PROP/TYPE6 (SOl_ORTH).
Global System Definition
- Definition 1: Solids, Isolid=1, 2, 17 + Iframe=0, 1 (default)
Global system is used, no element system (non-co-rotational formulation) available.
Element System Definition
- Definition 2: Solids, Isolid=1, 2, 17 + Iframe=2
Element system (with Iframe=2 co-rotational formulation) is used.
- Definition 3: Solids, Isolid=14 or 24
Iframe parameter has no effect. Element system is used, and co-rotational formulation defined already.