2D example: computation of Laplace's electromagnetic force
Introduction
This section depicts the computation of the mean and pulsating components of Laplace's force in 2D.
Definition: reminder
The Laplace's electromagnetic force is the force exerted on a conducting conductor placed in a magnetic field.
Mathematical expression
The force exerted on a conductor can be computed using Laplace's law:
![]()
where:
-
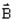 is the magnetic flux density in which the conductor
is placed
is the magnetic flux density in which the conductor
is placed -
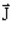 is the current density in the conductor
is the current density in the conductor
Expression of the mean and pulsating components of Laplace's force
The magnetic flux density and the current density in a point are expressed in the following way:
- Magnetic flux density
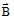 is written:
is written:
That is the parametric equation of an ellipse (see the figure beside)
- the current density
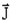 is written:
is written: 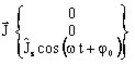
Thus , the expression of the Laplace's force in a point is:
![]()
![]()
Expression of the mean and pulsating components (continued)
Hence, the Laplace's force is constituted by:
- a mean component :
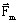
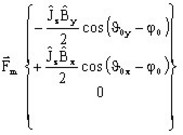
- a pulsating component :
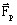
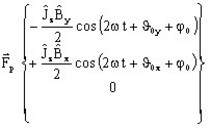
Elliptical representation
The force can be spatially represented as that in the figure below.
- The mean component
 is defined by:
is defined by:- its modulus and its orientation with respect to the Ox axis( α angle)
- The pulsating component
 described by an ellipse of 2ω pulsation:
described by an ellipse of 2ω pulsation:- major axis: a
- minor axis: b
- orientation of the ellipse with respect to the Ox (β angle)