Vector quantities
Introduction
The quantities available for post-processing can be scalar or vector quantities.
This section deals with vector quantities and recalls some definitions: complex notation, elliptical representation…
Vector quantities (complex notation as rotating vectors)
Each component of a vector quantity can be written as a sinusoidal quantity:
![]() ; …
; …
or, in complex notation:
![]() ; …
; …
![]() ; …
; …
where:
-
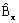 is the modulus of the complex component
is the modulus of the complex component 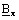
-
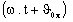 is the argument (or the phase) of the complex
component
is the argument (or the phase) of the complex
component 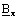
-
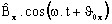 is the real part of the complex component
is the real part of the complex component 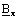
-
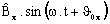 is the imaginary part of the complex component
is the imaginary part of the complex component 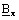
Elliptical representation in 2D
In general case, the vector quantities are varying in function of time on ellipses.
For each point, the magnetic flux density ![]() can be written:
can be written:
![]()
![]()
These are the parametric equations of an ellipse.
The two components of the magnetic flux density ![]() can be expressed depending on the ellipse characteristics,
as follows:
can be expressed depending on the ellipse characteristics,
as follows:
-
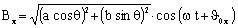 , where
, where 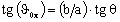
-
where
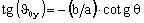
a is called “½ major axis” and b is called “½ minor axis”