Initialization by static calculation: particular cases
General case
The static initialization permits a computation close to reality (without numeric transient) in the cases where there are non-null sources of field at the initial time t = 0 s: magnets, currents (constant, three-phase...)
Particular cases
There are a number of situations in which there are:
- non-null sources of field at the initial time t = 0 s (as described previously)
- and a change in the state of the circuit at t = 0 s
- Contactor (establishment of the voltage at t = 0 s)
- Closing switch
- Discharge of capacitor
These particular situations are presented in the blocks below.
Contactor
Contactor with magnet; with establishment of the voltage at t = 0 s :
- initialization by static calculation allows to take into account the flux generated by the magnets
-
to respect the "assumptions associated with the initialization by static calculation", the voltage should be set at t = 0 + epsilon
⇒ voltage is described with the function Valid or the function ValidLR as presented in the figure below
| Finite element description: | Circuit description: |
|---|---|
|
|
|
| Coil around the core and the magnet is not represented |
U(t) = U0*Valid(t, 1e-8,) U(t) = U0*ValidLR(t,0, ,0,0) |
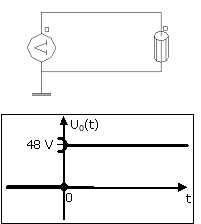
Switch
Device with magnet, and electrical circuit with a switch closes at t = 0 s :
- initialization by static calculation allows to take into account the flux generated by the magnets
-
to respect the "assumptions associated with the initialization by static calculation", the switch must be closed at t = 0 + epsilon
⇒ see examples below
|
|
|
| U0(t) = 48*ValidLR(t,0,,0,0) | U0(t) = 5*cos(ω*t)*ValidLR(Time,0,,0,0) |
Capacitor
Device with magnet, and electrical circuit with discharge of a capacitor at t = 0s :
- initialization by static calculation allows to take into account the flux generated by the magnets
- to respect the "assumptions associated with the initialization by static calculation", you must:
- add a switch in series with the capacitor
- open the switch at t = 0 + epsilon