Beam Elements (TYPE3)
Radioss uses a shear beam theory or Timoshenko formulation for its beam elements.
- No cross-section deformation in its plane.
- No cross-section warping out of its plane.
With these assumptions, transverse shear is taken into account.
This formulation can degenerate into a standard Euler-Bernoulli formulation (the cross section remains normal to the beam axis). This choice is under user control.
Local Coordinate System
The properties describing a beam element are all defined in a local coordinate system.
This coordinate system can be seen in Figure 1. Nodes 1 and 2 of the element are used to define the local X axis, with the origin at node 1. The local Y axis is defined using node 3, which lies in the local XY plane, along with nodes 1 and 2. The Z axis is determined from the vector cross product of the positive X and Y axes.
The local Y direction is first defined at time and its position is corrected at each cycle, taking into account the mean rotation of the X axis. The Z axis is always orthogonal to the X and Y axes.
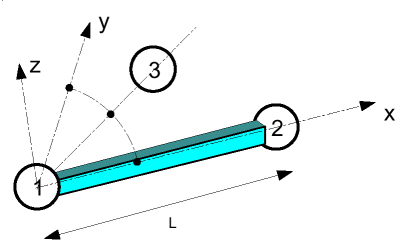
Figure 1. Beam Element Local Axis
Beam Element Geometry
- Cross section area
- Area moment of inertia of cross section about local x axis
- Area moment of inertia of cross section about local y axis
- Area moment of inertia of cross section about local z axis
Minimum Time Step
Where,
is the speed of sound: ,
,
Beam Element Behavior
- Membrane or axial deformation
- Torsion
- Bending about the z axis
- Bending about the y axis
Membrane Behavior
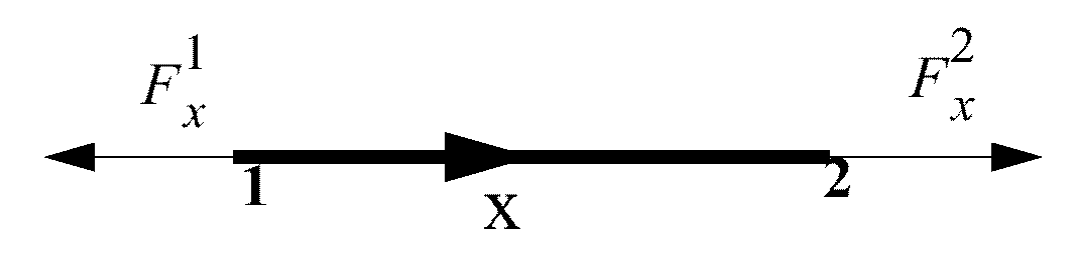
Figure 2. Membrane Forces
- Elastic modulus
- Beam element length
- Nodal velocity in x direction
Torsion
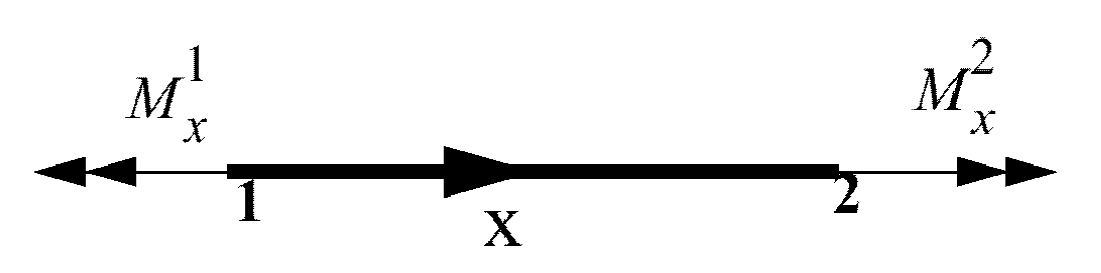
Figure 3. Torsional Loading
- Modulus of rigidity
- Angular rotation rate
Bending About Z-axis
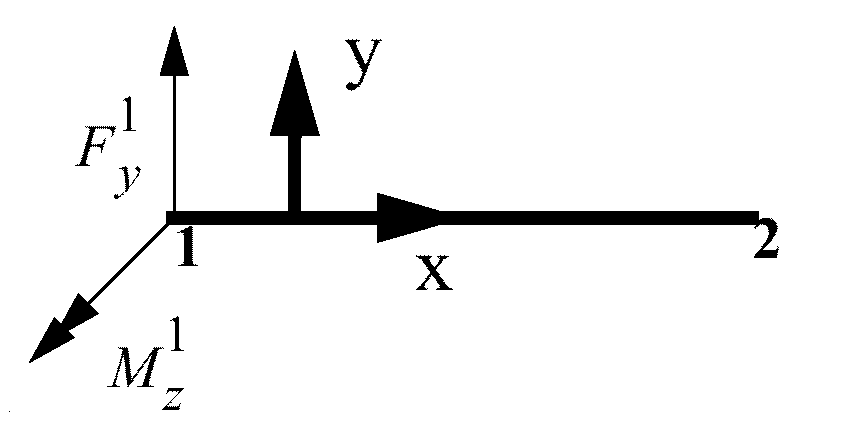
Figure 4. Bending about the Z Axis
Where,
,
is the Poisson's ratio.
The factor takes into account transverse shear.
Bending About Y-axis
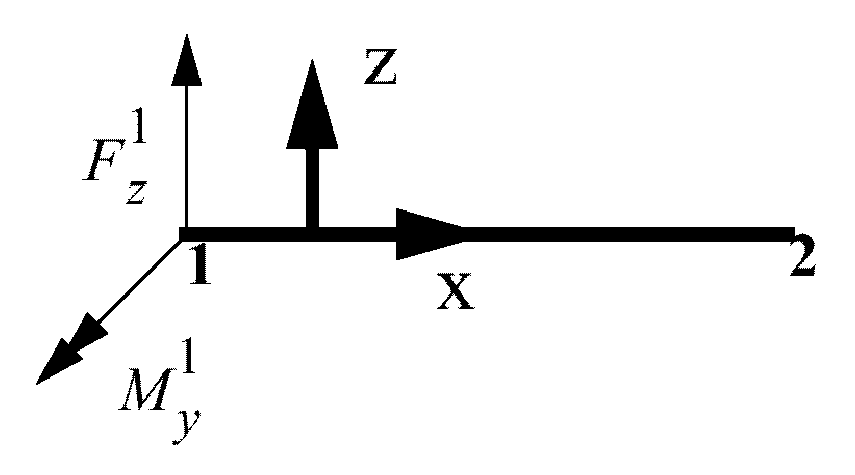
Figure 5. Bending about Y Axis
Where, .
Like bending about the Z axis, the factor introduces transverse shear.
Material Properties
- Elastic
- Elasto-plastic
Elastic Behavior
The elastic beam is defined using material LAW1 which is a simple linear material law.
The cross-section of a beam is defined by its area and three area moments of inertia , and .
Elasto-plastic Behavior
A global plasticity model is used.
However, this model also gives good results for the circular or ellipsoidal cross-section. For tubular or H cross-sections, plasticity will be approximated.