ランダム荷重下での構造の疲労寿命のスタディ。
ランダム応答解析のパワースペクトル密度(PSD)結果を使用して、応力範囲に対するサイクル数の確率密度関数を生成するために使用されるモーメント
を計算します。
PSDモーメントは、ランダム応答解析から生成されるPSD応力に基づいて計算されます。
パワースペクトル密度(PSD)モーメント
PSDモーメントは、ランダム応答解析から生成される応力PSDに基づいて次のように計算されます:
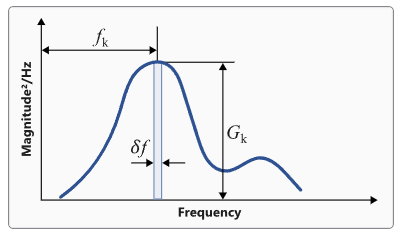
Figure 1. PSDモーメントの計算
モーメントは以下に基づいて計算されます:
(1)
各値の意味は次のとおりです:
-
- 周波数の値。
-
- 周波数
におけるPSD応答値。
応力範囲の発生確率の計算
各ビンセクション内の最初と最後の応力範囲値の間での応力範囲の発生確率の計算は、ユーザーが定義します。
と
間で応力範囲が生じる確率
は次のようになります:
(2)
確率密度関数(応力範囲に対するサイクル数の確率密度)
上記のとおり計算されたPSDモーメントは、応力範囲の確率密度関数
の生成に使用されます。この関数は、指定された損傷モデルに基づきます。DIRLIK、LALANNE、NARROW、およびSteinberg 3 band(THREE)オプションを損傷モデルの定義に使用できます。
- DIRLIK
- DIRLIKでは、確率密度関数を決定するため、次のような閉形式解を仮定しています。(3)
- 各値の意味は次のとおりです:
-
-
-
-
-
-
-
-
- 不規則度指数。
-
- 応力範囲。
- LALANNE
- LALANNEランダム疲労損傷モデルは、確率密度関数を次のように表します:(4)
- 各値の意味は次のとおりです:
-
- 不規則度指数。
-
- 応力範囲。
- NARROW
- 狭帯域ランダム疲労損傷モデルは、次の確率関数を使用します:(5)
- 各値の意味は次のとおりです:
-
- 応力範囲。
- 狭帯域では、デフォルトで、ゼロクロッシングの数
がピークの数
の代わりに使用されます。これは、
を含む数値計算は、数値的に不安定になる場合があるためです。信号が理想的な狭帯域であれば、ゼロクロッシングの数とピークの数はほぼ等しくなるはずです。
- THREE
- Steinberg 3-bandランダム疲労損傷モデルは、次の確率関数を使用します:(6)
- 各値の意味は次のとおりです:
-
- 応力範囲。
- 他の損傷モデルとは異なり、THREE帯では、これらの値は確率であり、確率密度ではありません。これは、他の損傷モデルでは小文字の
が使用されているのに対し、大文字の
が使用されていることからも明らかです。
- THREE損傷モデルでは、これらの確率は、
に時刻歴全体におけるゼロクロッシングの総数を掛けることで、直接サイクル数の計算に使用されます。その他の損傷モデル(THREEを除く)の場合、まず、確率密度の値に、
(ビンサイズ)を掛けて確率を求めます。
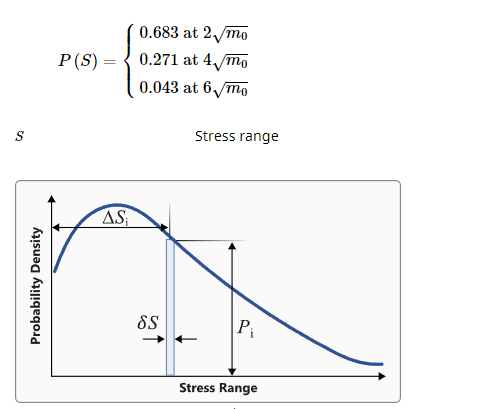
Figure 2. 確率密度関数. 応力範囲に対するサイクル数の確率密度
- 確率密度関数は、ランダム応答疲労解析設定で定義される次のパラメータに基づいて調整できます。
Upper Stress Range Factor
応力範囲の上限を次のように計算します:
応力範囲の上限 = 2*RMS Stress*Upper Stress Range Factor
RMS Stressは、ランダム応答サブケースの出力です。着目する応力範囲は、応力範囲の上限で制限されます。この上限を超える応力は、ランダム疲労損傷計算で考慮されません。
Upper Stress Range
応力範囲の上限を直接指定します。
Number of Bins
確率の計算対象となる応力範囲の幅
を計算します(Figure 2を参照)。デフォルトは100で、最初のビンは0.0から始まり、
までとなります。応力範囲の幅は、DS=Upper stress range/Number of binsで計算されます。
Stress Range Width
応力範囲の幅(
)を直接定義します。
応力範囲の発生確率の計算
各ビンセクション内の最初と最後の応力範囲値の間での応力範囲の発生確率の計算は、損傷モデルに基づきます。
- DIRLIK、LALANNE、NARROW
-
と
間で応力範囲が生じる確率
は次のようになります: (7)
- THREE
- Equation 6をご参照ください。
- THREE損傷モデルの場合、ビンは3つのみです。各応力範囲(2*RMS、4*RMS、および6*RMS)でのサイクル数は、対応する確率にゼロクロッシングの総数を直接掛けることで算出されます(ゼロクロッシングの数の計算については、以下の項をご参照ください)。
損傷モデルの選択
損傷モデルの選択に役立つ可能性のある情報を以下に示します。
- 応力のPSDモーメントは、対応するモーメントの計算に使用され、このモーメントは応力範囲の確率密度関数を求めるために使用されます。
- DIRLIKおよびLALANNEモデルは、分布がより広範な応力範囲スペクトラムでの確率を生成します。したがって、これらのモデルは、入力のランダム信号が、複数の周波数にわたるさまざまな応力範囲で構成される場合に使用されます。DIRLIKおよびLALANNEが使用される場合、確率密度関数内の情報は、応力範囲分布のより広い範囲をより適切に捉えます。
- NARROWモデルは、応力範囲が高い確率で特定の応力範囲分布と密接に関連していることが期待されるランダム信号を対象としています。したがって、入力のランダムデータの応力範囲分布が広くなく、特定の応力範囲に集中していることがわかっている場合は、NARROWを選択してください。このモデルは、この特定の応力範囲、またはその周辺で、応力範囲の確率が最も高くなることを期待しています。
- THREEモデルはNARROWモデルに似ていますが、ランダム信号の分布に、1*RMSとの関連に加え、2*RMSおよび3*RMSとの関連(ただし、関連性は小さい)が含まれます。したがって、入力のランダムデータが主に1*RMSの応力範囲、そして程度は低いものの2*RMSと3*RMSに集中している場合は、THREEを選択してください。
ピークおよびゼロクロッシングの数
- NARROW、THREE
- 元の時間用域ランダム荷重(周波数ベースのランダムPSD荷重はここから生成されます)において、1秒あたりのゼロクロッシングの数は次のように表されます:(8)
各値の意味は次のとおりです:
-
- 計算される、対応するモーメント。
- DIRLIK、LALANNE
- 元の時間用域ランダム荷重(周波数ベースのランダムPSD荷重はここから生成されます)において、1秒あたりのピークの数は次のように表されます:(9)
各値の意味は次のとおりです:
-
- 計算される、対応するモーメント。
サイクル数
- NARROW帯、THREE帯
- サイクルの総数は、次のように計算されます:(10)
各値の意味は次のとおりです:
- T
- 総露出時間。
- DIRLIK、LALANNE
- サイクルの総数は、次のように計算されます:(11)
各値の意味は次のとおりです:
- T
- 総露出時間。
- 特定の応力範囲のサイクル総数
- 応力範囲が
であるサイクルの総数は、次のように計算されます:(12)
疲労寿命と損傷
疲労寿命(破壊までのその材料の特定の応力範囲
のサイクル最大数)は、その材料のSN曲線に基づいて、次のように計算されます:
(13)
ランダム荷重を適用した結果としての合計疲労損傷は、次のように計算されます:
(14)
ゼロでない平均応力をもたらす、荷重による平均応力補正を考慮するには、そのような荷重(一般には重力荷重)で構成される静的サブケースを定義します。この静的サブケースは、ランダム疲労解析のイベントセットアップで参照できます。

