Explanation of results
Conduction current and displacement current
The density of the conduction current is given by the post-processing parameter J2, which corresponds to the following formula:
![]()
The density of the total current (conduction current and displacement current) is given by the post-processing parameter JT2, which corresponds to the following formula:
![]()
Powers: general overview
As to the power, we distinguish the following quantities: the apparent power (S), the active power (P) and the reactive power (Q).
The complex apparent power S is the complex quantity: S = P + j Q
In Flux 3D, these quantities are expressed using the following relations:
-
the density of apparent power is given by the formula:
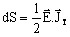 , i.e.
, i.e. 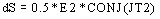
-
the density of active power dP corresponds to the real part of dS:
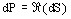 , i.e.
, i.e. 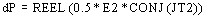
-
the density of reactive power dQ corresponds to the imaginary part of dS:
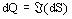 , i.e.
, i.e. 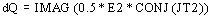
The computation of the previous quantities apparent power (S), active power (P) or reactive power (Q) are obtained by the Integral command of the explicit formulas from above.
Other possibilities are available to the user for the computation of the active and reactive power; these are presented in the following blocks.
Active power
The density of active power (average value) at a point is expressed using the quantities E and J by the relation:
![]()
The active power (average value) in a volume region is equal to:
![]()
Electrostatic energy
The density of electrostatic energy (average value over a period) at a point is expressed using the quantities D and E by the relation:
![]() ,
,
which for a linear and isotropic medium becomes:
The electrostatic energy (average value over a period) in a volume region is the
integral: ![]()
Reactive power
The relation between the density of the reactive power (dQ) and the density of the electric energy (dWe) is the following: dWe=dQ/2ω
The reactive power in a volume region can be computed by the formula: Q=2ωWe