Explanation of results: Flux and Inductance (theoretical)
Flux: definition
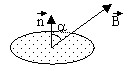
Consider a surface S placed in a magnetic field ![]() . The flux of the magnetic
flux density
. The flux of the magnetic
flux density ![]() across
the surface S is written:
across
the surface S is written: ![]() .
.
Magnetic flux across a random surface
For a surface perpendicular to the flux and a
homogeneous flux density on the surface the result is: ![]() .
.
For a surface whose normal ![]() is oriented randomly with respect to the flux density, the elementary
magnetic flux is:
is oriented randomly with respect to the flux density, the elementary
magnetic flux is: ![]() .
.
Thus, the flux across a random surface will be the surface integral: ![]()
In 3D, if the surface is in contact with two regions modeled by different magnetic scalar potentials, the results on each side of the surface can be different. This is explained by the fact that the modeling with scalar potentials does not ensure definitively the continuity of the normal component Bn of the magnetic flux density, but it ensures that of the tangential component Ht of the magnetic field intensity (unlike the vector model that ensures the local continuity of Bn, but not that of Ht).
Flux in a coil
In the case of a coil having N turns, the magnetic flux across the coil has the expression:
![]()
where:
![]() is the magnetic flux
“seen” by a turn and
is the magnetic flux
“seen” by a turn and
![]() is the total magnetic
flux in the coil, “seen” by N turns
is the total magnetic
flux in the coil, “seen” by N turns
We can compute the flux within a coil by computing the flux across a surface corresponding approximately to the coil geometry. This method is not accurate, but can be sufficient, in particular for a mutual flux computation. Other methods of magnetic flux computation are presented in the next paragraphs.
Self-inductance of a coil
The self-inductance of a coil k passed by a current Ik and crossed by the total magnetic flux Φk is given by the relation:
![]()
that for a linear problem can be written in the form:
![]()
Mutual inductance between two coils
The mutual inductance between two coils j and k is given by the relation:
![]()
which for a linear problem can be written in the form:
![]()
where:
- Φj is the magnetic flux in the coil j (non-supplied)
- Ik is the current in the coil k