Modèles de pertes fer

Introduction

Dans Flux, les modèles de pertes fer sont uniquement applicables sur des régions laminées, de ce fait, l'induction utilisée dans ces modèles est l'induction homogénéisée dans le paquet de tôles définie par :

${\mathit{B}}_{\mathit{h}}=K_f{\mathit{B}}_{\mathit{f}}+\left(1-K_f\right){\mathit{B}}_{\mathit{a}}$

En présence de champs tournants la caractéristique By = f(Bx) peut prendre la forme d'une ellipse il est donc plus judicieux de décomposer le vecteur de l'induction homogénéisé de la sorte :

${\mathit{B}}_{\mathit{h}}=\left[\begin{array}{c}{B}_{\backslash \backslash }\\ B_{⏊}\end{array}\right]$

Ces deux axes correspondent au petit et grand axes de l’ellipse décrite dans la figure : Figure 1

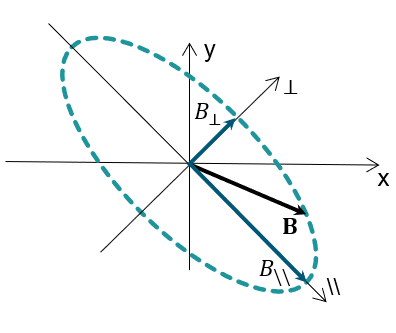
Figure 1. Caractéristique By = f(Bx)

Modèle de Bertotti modifié

Présentation du modèle :

La théorie de Bertotti nous donne l’expression des pertes en fonction de la fréquence et de l’induction.

La densité de puissance en transitoire s’exprime à l’aide de la relation :

$dP\left(t\right)=K_f\left(k_{1 }f{\left(\frac{∆B_{\backslash \backslash }+ ∆B_{⏊}}{K_f}\right)}^{{\alpha }_1}+k_{2 }g\left({\alpha }_2\right)\frac{1}{{K_f}^{{\alpha }_2}}{\left|\frac{d{B}_h}{dt}\right|}^{{\alpha }_2}+k_3 g\left({\alpha }_3\right)\frac{1}{{K_f}^{{\alpha }_3}}{\left|\frac{d{B}_h}{dt}\right|}^{{\alpha }_3}\right)$

$g\left({\alpha }_i\right)= \frac{2}{{\left(2\pi \right)}^{{\alpha }_i-1} 4\int {cos}^{{\alpha }_i}\left(\theta \right) d\theta }$

*La séparation entre les pertes supplémentaires ou en excès et les pertes classiques est artificielle. Elles peuvent être regroupées en un seul terme et correspondent alors aux courants induits réels se développant dans la tôle.

Un fichier Excel permettant de déterminer les coefficients ainsi que les exposants (Outil d'identification pour le modèle de Bertotti modifié) est disponible au chemin suivant :

DOSSIER_INSTALLATION\Flux\DocExamples\Tools\BertottiLossesCoefficients

dans lequel DOSSIER_INSTALLATION représente le dossier d’installation de Flux sur la machine.

Afin de lancer l'outil d'identification pour le modèle de Bertotti modifié, ouvrir le fichier BertottiLossesCoefficients.xls.

Limite de validité

Dans l'application magnéto-harmonique, l'expression de la densité de perte est la suivante :

$dP=\left(k_1 B_{max}^{{\alpha }_1} f+{k_2 {(B}_{max} f)}^{{\alpha }_2}+{k_3 {(B}_{max} f)}^{{\alpha }_3} \right)K_f$

Le logiciel utilise la valeur de l'induction en chaque point. Par conséquent, il convient d’être très prudent avec les résultats concernant les problèmes représentant des machines tournantes avec l'application Magnéto Harmonique. En effet, pour ce type de modélisation, le rotor est fixe et le mouvement est introduit en modifiant la résistivité des conducteurs au rotor. Ainsi, l'induction calculée est effectivement maximale en un point pour cette position donnée du rotor par rapport au stator à cause des harmoniques d’espace. Il s'ensuit que, l'induction calculée ne correspond pas à l'induction maximale que l’on obtiendrait sur une période si le rotor tournait. En conséquence, le calcul des pertes doit être utilisé dans ce cas avec beaucoup de précaution.

De plus, dans le cas d’une approximation non linéaire pour la loi de comportement B(H), la saturation, introduite à l’aide d’un modèle équivalent peut altérer les valeurs locales de l’induction.

Étapes de définition du modèle de Bertotti modifié dans le matériau

Modèle LS

Présentation du modèle :

Surface caractéristique H(B, dB/dt) :

Pour chacun des matériaux, la surface caractéristique H(B,dB/dt) est relevée sur un banc de type Epstein adapté à des essais à moyenne fréquence.

Un exemple de ce type de surface est représenté sur la figure ci-dessous.

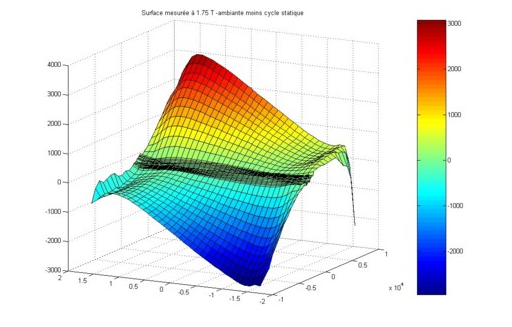
Figure 2. Surface H(B, dB/dt)

Reconstruction du cycle :

Un modèle analytique permet de reconstituer le champ H à partir des valeurs de B :

H(B,dB/dt) = Hstatique(B) +Hdynamique (B,dB/dt)

Des courbes B(H) de ce type peuvent alors être obtenues, permettant des calculs de pertes fer assez précis.

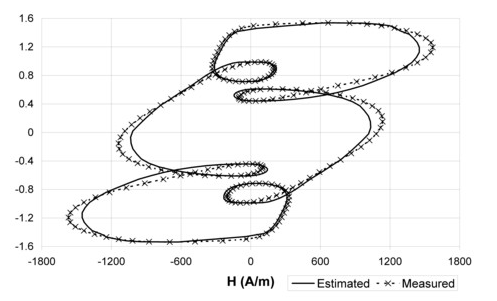
Figure 3. Induction sinusoïdale & 5ème harmonique à 200Hz

Le modèle LS est réservé aux différentes nuances de tôles qui ont été caractérisées spécialement.

Matériaux disponibles dans Flux :

Pour plus d'informations à propos des tôles magnétiques, voir cette page : Désignation des tôles magnétiques

Avec ce modèle, l'utilisateur peut également importer lui même ses matériaux, voir Identification du modèle LS avec MILS

Définition du modèle du modèle LS dans le matériau

Voir la section suivante : Matériau doux isotrope : Tôles décrites par le modèle LS