Linear Stability
The stability of solution concerns the evolution of a process subjected to small perturbations. A process is considered to be stable if small perturbations of initial data result in small changes in the solution. The theory of stability can be applied to a variety of computational problems.
The numerical stability of the time integration schemes is widely discussed in the Theory Manual. Here, the stability of an equilibrium state for an elastic system is studied. The material stability will be presented in an upcoming version of this manual.
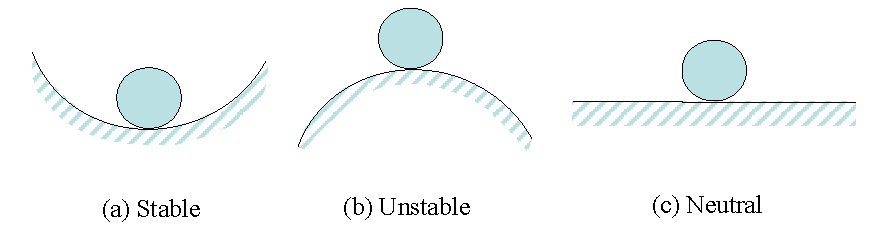
図 1. Schematic Presentation of Stability
It is clear that the state (b) represents an unstable case since a small change in the position of the ball results the rolling either to the right or to the left. It is worthwhile to mention here that stability and equilibrium notions are quite different. A system in static equilibrium may be in unstable state and a system in evolution is not necessary unstable.
A good understanding of the stability of equilibrium can be obtained by studying the load-deflection curves. A typical behavior of a structure in buckling is given in 図 2. The load-deflection curves are slightly different for systems with and without imperfection. In the first case, the structure is loaded until the bifurcation point B corresponding to the first critical load level. Then, two solutions are mathematically acceptable: response without buckling (BA), response after buckling (BC).
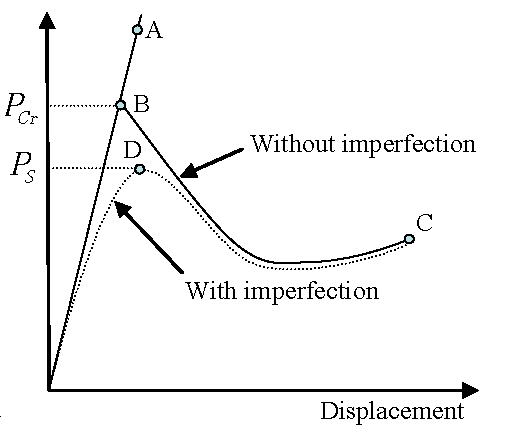
図 2. Bifurcation and Limit Points in Load-Deflection Curves for System With and Without Imperfections. B: Bifurcation point, D: Limit point
General Theory of Linear Stability
The principle of virtual power and the minimum of total potential energy are the various mathematical models largely used in Finite Element Method. Under small-perturbations assumption these notions can be applied to the equilibrium state in order to study the stability of the system.
- Static equilibrium
-
(1)
- Stable (case a)
-
(3) - Unstable (case b)
-
(4) - Neutral stability (case c)
-
(5)
- Designate element
- Vector of the external forces
- Virtual displacement vector
- Green-Lagrange strain tensor
- Piola-Kirchhoff stress tensor
The equation 式 9 is written as a function of X, the displacement between the initial configuration and the critical state . If and are the linear response obtained after application the load in the initial configuration , in linear theory of stability suppose that the solution in for the critical load is proportional to the linear response:
- Stiffness matrix
- Initial displacement matrix
- Initial stress or geometrical stiffness matrix
- Elastic matrix
Linear stability assumes the linearity of behavior before buckling. If a system is highly nonlinear in the neighborhood of the initial state , moderate perturbations may lead to unstable growth. In addition, in case of path-dependent materials, the use of method is not conclusive from an engineering point of view. However, the method is simple and provides generally good estimations of limit points.
The resolution procedure consists in two main steps. First, the linear solution for the equilibrium of the system under the application of the load is obtained. Then, 式 14 is resolved to compute the first desired critical loads and modes. The methods to compute the eigen values are those explained in Large Scale Eigen Value Computation.