Application Area 6: Optimize Dynamic Response
Often the task of optimization is to find the values of some design variables so that the dynamic response is optimized in some way.
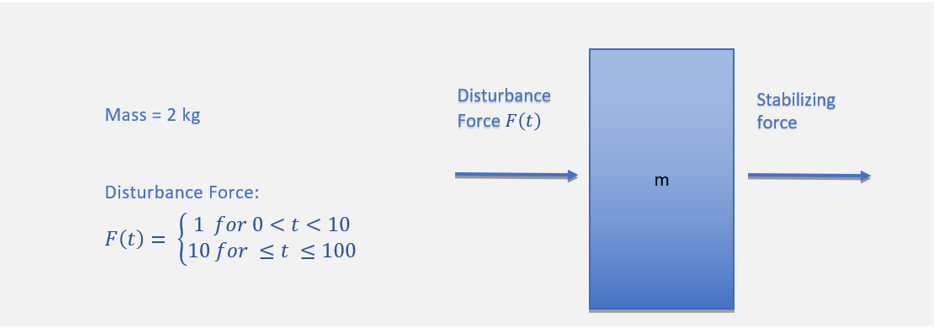
Figure 1.
The figure above shows a simple representation of a stabilizer. The stabilizer is basically a PID controller that prevent the mass from deviating from its initial point. The disturbing force is a time variant function.
- Objective
- Minimize the integral of displacement magnitude, velocity magnitude and acceleration magnitude over time. Keep the value of gains under a certain number. (This is done by adding constraints).
- Design Variables
- Three gains of PID controller
. Note: For this example, finite differencing is used to compute the sensitivities. The code with detailed explanation is provided in the PID Controller Example section.