DebugOutput
Command ElementThe DebugOutput command generates debugging output from MotionSolve. These extra diagnostics are typically used to understand MotionSolve analysis failures, so that modeling issues may be fixed and simulation parameters may be changed to get past the failure(s).
Description
- Tracing the time-step algorithm and convergence history of the Newton-Raphson iterations for statics, quasi-statics and dynamics.
- Outputting animation information at each iteration so that a convergence history can be visually examined.
The attributes below are used to identify and fix modeling issues.
Format
<DebugOutput
[ switch_on = "TRUE" || "FALSE" ]
[ debug_anim = "TRUE" || "FALSE" ]
[ screen_output = "TRUE" || "FALSE" ]
/>Attributes
- switch_on
- A logical flag that controls the generation of debugging information about the solver analysis
steps, especially regarding the Newton-Raphson numerical method used by statics, quasi-statics
and dynamics. This messaging can be used to identify the modeling entities that cause the
largest convergence error. For a MotionSolve failure, look at the
entities that are giving the integrator trouble right before the solver fails and investigate
these first. Generally, assuming that there is no modeling error, look for discontinuities in
the model, and read the error messaging that MotionSolve reports.
This parameter can have values of "TRUE" or "FALSE".
- "TRUE" specifies that at every iteration, additional debug information is output to the screen and the log file.
- "FALSE" specifies that additional debug information is not output to the screen and the log file.
- debug_anim
- A logical flag that controls the generation of animation frames at each iteration for debug
purposes. This animation is often helpful to determine how the models is being corrected (that
is, repositioned) in Newton-Raphson and possibly give you clues on how to change the modeling
or MotionSolve settings to find a converged solution. It can have
values of "TRUE"
or "FALSE".
- "TRUE" specifies that at each iteration, additional animation information is output to the H3D file.
- "FALSE" specifies that no additional animation information is output to the H3D file.
- screen_output
- A logical flag that controls where the debug output information is written. Choose between "TRUE" or "FALSE".
- "TRUE" specifies that the debug information is written to the screen as well as to the log file.
- "FALSE" specifies that the debug information is written only to the log file.
Example
<DebugOutput
switch_on = "TRUE"
/>Comments
- Newton-Raphson Method
At the center of most of the output that comes from this command is a numerical method called Newton-Raphson (N-R). This method is used to solve a set of non-linear algebraic equations (NLAE's). This is a well-known method, often called "Newton's method," and you can find many sources that describe it. This method finds the roots of the NLAE's. N-R is part of the solution process called the "corrector," as it corrects an initial value to find a better solution to the NLAE's.
N-R uses the partial derivatives of the non-linear algebraic equations with respect to the states of the system (the sensitivities) with the intent to progressively find a solution to the equations with less and less error. The matrix of partial derivatives of these equations with respect to the states is called the "Jacobian"; thus, the Jacobian is essential to solving the N-R method.
In statics, quasi-statics, and dynamics, the equations of motion are converted into a set of non-linear algebraic equations (statics and quasi-statics, by virtue of setting all rates to zero; dynamics, by virtue of the integration method). At each iteration, N-R tries to find a solution to the NLAE within the error tolerance. If the solution is not within the error tolerance, N-R updates the states using the Jacobian and tries to find a better solution. This process repeats until the error tolerance is met or the maximum number of iterations is exceeded.
In dynamics, if the maximum number of iterations is exceeded, the solver may try to take a smaller step size and attempt to solve the equations of motion again. If, however, the integrator cannot cut the step size any more, the analysis will fail. In statics, if the maximum number of iterations is exceeded, then the analysis fails, and you should examine the output from this command.
A very good way to understand N-R is to see it visually. Below is a plot of a non-linear algebraic equation, y= f(x). This image shows an equation with one variable, but this is generally applicable to equations with any number of variables.
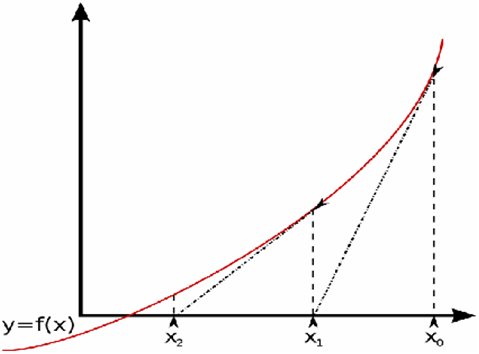
Figure 1. Newton-Raphson MethodThe equation can always be re-written such that f(x) = 0, and this is what N-R is solving to find the root, x*, such that f(x*) < error tolerance.
Here, the initial guess for the state x is x0. If f(x0) > error tolerance (that is, it does not satisfy the error), then N-R computes the linear equation for f(x0) at x0, and uses this to compute a (hopefully) better solution at x1. This new state, x1, is used to evaluate f(x1) and see if this is within the specified error tolerance. You can see that for a non-linear equation like the example here, repeated iterations with N-R will become more and more accurate. For some non-linear equations, this is not the case and N-R can actually diverge.
The slope of the linear equation (dotted line in the figure) used to update to the next state is effectively the Jacobian matrix - the partial derivatives of all equations with respect to the states in the system. Updating the Jacobian at each iteration is generally a computationally expensive process, so sometimes this matrix is reused from prior iterations since the overall solution process is more efficient .
The debugging output you get with switch_on and debug_anim shows the N-R convergence information in table and graphical form, respectively. When the solution does not converge, you should try to better understand what is going on in the model to either add, remove, or fix a modeling entity, changing the MotionSolve settings for the analysis. Problems can arise if either the Jacobian does not have good information - which is the case for modeling entities that are discontinuous (non-smooth) or if the initial configuration of the system is far away from the final solution.
More details can be found in the subsequent comments.
- switch_onswitch_on potentially generates a lot of information and there is a significant performance penalty associated with its use. Consequently, it should be used only when a model is being debugged. See Comment 5 for more detail on the output that is generated. This output may be used to further understand and diagnose the following scenarios:
- Corrector failures
- Integration failures
- Small step sizes
- Low integration orders
- debug_anim
This attribute is intended to aid visual debugging of a static analysis via the animation H3D in the HyperView post-procesor. The attribute debug_anim writes out results at each iteration of the static simulation to the animation H3D and the output MRF file. This parameter should only be used while debugging a static simulation. If you set debug_anim to "TRUE" and run multiple simulations, MotionSolve quits with a warning message.
If you would like to debug a static analysis in a model that contains many analyses, you can use the <Save> and <Load_Model> command statements to isolate the static simulation that is of interest. Then you can use the debug_anim attribute to visually debug the convergence for static equilibrium.
Setting debug_anim to "TRUE" also potentially generates a lot of information and creates large H3D files. There is significant performance penalty associated with its use. Consequently, it should be used only when a model is debugged.
- switch_on = "TRUE"
output
Figure 2 below shows the typical output in the log file when the attribute switch_on is set to v.
Figure 2. Convergence History for a Quasi-static AnalysisFigure 2 shows the details of the Newton-Raphson convergence history of the solution process for a step during a quasi-static analysis performed with a FIM_D.
At the top, the time step history is shown. Referring to Figure 2 above, the information (shown in brick-red text) provided includes:- The current time at which a solution has been obtained, Tn=3.17964E+01.
- The step size being attempted, Step=4.47657E-01.
- The new time if the solution is successful, Tn+1=3.22441E+01.
- The integrator order, Order=3.
This is followed by the convergence history for the step. Information about each iteration is contained in one line. The data is column-ordered for easily identifying the information. Once again, using Figure 2 as a reference, the data in each line includes:
- The iteration count. This tells you how many iterations have been performed by N-R.
- The maximum residual (error) in equations of motion.
- The index of the equation that has the largest error .
- The modeling component that has the largest residual.
- The maximum change calculated by the Newton-Raphson iteration.
- The index of the state that has the largest change.
- The modeling component that has the largest change.
- Whether the Jacobian has been evaluated for this iteration or not. A "J" at the end of a line indicates that a new Jacobian has been
evaluated.
When there is a modeling error, or a parameter value, such as bushing stiffness, is off scale, the debug data can be used to identify which modeling element may have the error. Note that this is a symptom of the problem, not necessarily the entity that needs to be changed in the model. For example, consider a rack and pinion-steering system with a coupler constraint that couples the rotational motion of the steering system to the translational motion of a rack. If the coupler constraint is defined incorrectly, and tries to move the rack in a manner not intended, you may see the largest error reported in the rack body and/or constraints, rather than the problem in the coupler constraint itself.
The following table lists the short forms used to reference the commonly used modeling components.Short Form Variation Description Parent Modeling Element Constraint Elements APJt At Point Joint Constraint_Jprim CVJt Constant Velocity Joint Constraint_Joint CJ Contact Joint Internal Representation CP Coupler Constraint_Coupler CVCV XI, YI, ZI XJ, YJ, ZJ
Position Constraints for Curve to Curve Joint Constraint_CVCV CVSF XDI, YDI, ZDI, XDJ, YDJ, ZDJ Derivative of position constraints for Curve to Surface Joints Constraint_CVSF CYJt Cylindrical Joint Constraint_Joint DCV X, Y, Z Deformable Curve functions in X, Y and Z Reference_DeformCurve FXJt Fixed Joint Constraint_Joint FRJt Free Joint Constraint_Joint GR Gear Joint Constraint_Gear GCON General Constraint Constraint_General HKJt Hooke Joint Constraint_Joint ILJt Inline Joint Constraint_Joint IPJt Inplane Joint Constraint_Joint ORJt Orientation Joint Constraint_Joint PAJt Parallel Axes Joint Constraint_Joint PRJt Perpendicular Joint Constraint_Joint PLJt Planar Joint Constraint_Joint PC XJ, YJ, ZJ Curve Function Constraint Reference_ParamCurve PS X, Y, Z Surface Function Constraint Reference_ParamSurface PTCV Point to Curve Constraint Constraint_PTCV PTSF Point to Surface Constraint Constraint_PTSF RVJt Revolute Joint Constraint_Joint BLJt Spherical Joint Constraint_Joint TRJt Translational Joint Constraint_Joint UVJt Universal Joint Constraint_Joint UCON User Constraint Constraint_UserConstr RB DJC Distance Jack Constraint Internal Representation FB DJC Distance Jack Constraint Internal Representation RB RTC Rigid Triad Constraint Internal Representation RB RFC Rigid Force Constraint Internal Representation RT Rigid Joint Triad Internal Representation FT Flexible Joint Triad Internal Representation SFSF Surface to Surface Constraint Constraint_SFSF ET Relative Triad Internal Representation MTN Joint Motion Constraint Motion_Joint MTNAUX Joint Motion Constraint (Time Variant Motion) Internal Representation MTNGC Joint Motion Generalized Coordinate Internal Representation MTNVAR Motion Marker Constraint Motion_Marker VAR_MT Joint Motion - Translation Internal Representation VAR_MR Joint Motion - Rotation Internal Representation VAR_MC Joint Motion - Cylindrical, rotation Internal Representation MTNAUX Joint Motion - Cylindrical, translation Internal Representation Diff Elements SDF Explicit Solver Diff Control_Diff SDIV Implicit Solver Diff Varcoord Control_Diff SDI Implicit Solver Diff Control_Diff CS X Control State Control_SISO Y Control Force Control_SISO LS X Linear State Control_StateEquation (Linear) Y Control Force Control_StateEquation (Linear) GS X Control State Control_StateEquation Y Control Force Control_StateEquation Force elements BM DX, DY, DZ Beam Force Force_Beam RX, RY, RZ Beam Torque FLD DX, DY, DZ Field Force Force_Field RX, RY, RZ Field Torque SF Scalar Force Force_Scalar TS Translational Spring Force_SpringDamper BSH FX, FY, FZ Bushing Force Force_Bushing TX, TY, TZ Bushing Torque VAR_F Vector Force Force_VectorOneBody Force_VectorTwoBody VAR_X Vector Force Internal Representation VAR_T Vector Torque Force_VectorOneBody Force_VectorTwoBody VAR_TQ Vector Torque Internal Representation VAR_TP Vector Torque Reaction Internal Representation VAR_ST Scalar Torque Force_ScalarTwoBody PFORCE Penalty Force Reference_Variable PFO Penalty Force of type User Variable Reference_Variable VAR_UFX User Vector Force/Torque Force_VectorOneBody Force_VectorTwoBody VAR_UFY VAR_UFZ VAR_UTX VAR_UTY VAR_UTZ VAR_US User Scalar Force Force_ScalarTwoBody VAR_FX User YForce and YTorque Force_StateEqn VAR_FY VAR_FZ VAR_TX VAR_TY VAR_TZ PB X, Y, Z Point Body Forces Body_Point RB X, Y, Z, RX, RY, RZ Rigid Body Forces Body_Rigid FB X, Y, Z, RX, RY, RZ Flexible Body Forces Body_Flexible NFO Multipoint Force Force_MultiPoint Other elements SV Solver Variable Reference_Variable In addition to the above, for the variable section (dark green in Figure 2), the element's short form may be appended by one letter. This letter indicates the kind of entity for which the maximum change is observed:
L - short name for Lambda, which refers to the constraint element terms.
A - short name for Acceleration, which refers to the acceleration terms (only for second order integrator).
V - short name for Velocity, which refers to the velocity terms.
D - short name for Displacement, which refers to the displacement terms.
- Understanding Corrector Failures
Figure 3 below depicts a sequence of iterations that is diverging. This results in a "Corrector Failure."
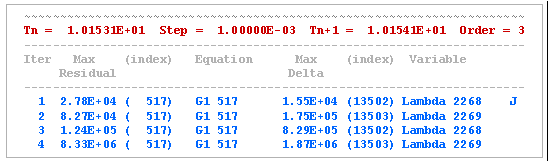
Figure 3. A Sequence of Diverging Newton-Raphson IterationsIn Figure 3, you can see that the error in the equations is not decreasing with each iteration; instead it is increasing. The debug information (shown in blue) also indicates that equation 517, contained by modeling element G1-517, seems to have the most difficulty. You can now go back to the input deck and try to understand why this could be so.
Conversely, if you see the error decreasing with each iteration, but the solver runs out of iterations (that is, exceeding the maximum number of iterations specified), then try to increase the maximum number of iterations to give the solver a chance to converge.
- Integration Failures
The corrector may be converging, but the integrator may be having difficulty satisfying the local error criterion. switch_on output may be used to understand why this is happening and help identify the root cause in the model.
Figure 4 below depicts a sequence of steps taken by DSTIFF using the Stabilized Index-1 formulation. Assume that an integration error tolerance of 1.0E-3 was specified.
switch_on output at Time=3.43331E-02 seconds is shown for illustration purposes.
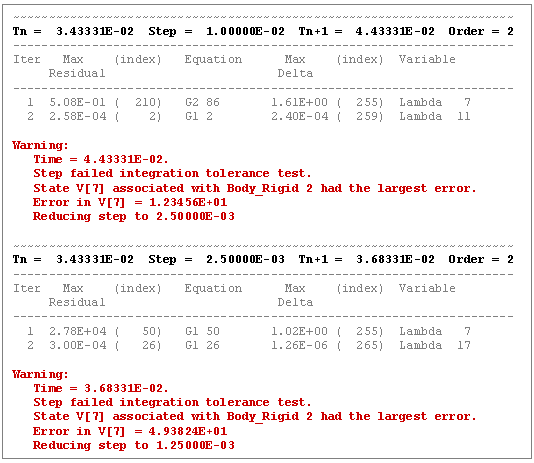
Figure 4. A Sequence of Failed Integration StepsThe switch_on information in Figure 4 makes it quite clear that the corrector is not having any difficulty in converging to a solution. However, the integrator is having difficulty satisfying the local error test. The output also makes it clear that a system velocity associated in Rigid_Body 2 is showing the largest error.
One possible cause could be that a discontinuous motion is acting on Rigid_Body 2. So, with this information, you can look at all Motion inputs on Rigid_Body 2. A non-differentiable motion (a signal with "sharp corners") is a likely cause, because the displacements seem to converge but the velocities are not.
- Small Step Sizes
switch_on output can also be used to determine whether the integrator is taking small steps and can help in identifying possible causes. Small integration steps are being taken when the integrator is either having corrector convergence difficulties or large integration errors. In either case, one can examine the output from switch_on and trace the difficulty back to a possible error or an unrealistic parameter (Mass, Stiffness, Damping, Discontinuity, and so on) in the model.
- Low Integration Orders
switch_on output can be used to detect and diagnose situations where the integrator is seemingly stuck at low integration orders. The history of each step can be examined and the order noted. If the order is low (for instance, Order=1 always) and the step size is small as shown in the example below, the situation is worth examining:
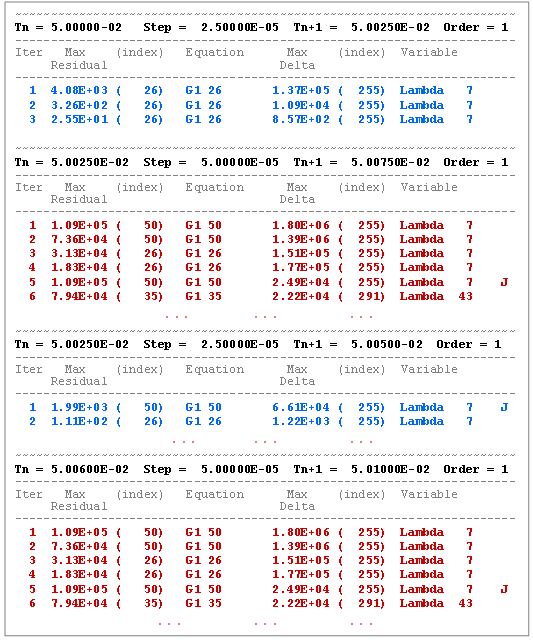
Figure 5. Simulation Stuck at Low Order and Step SizeIn Figure 5 above, switch_on output for a series of steps with an Index-3 DAE formulation with an error tolerance = 1.0E-3 is shown. You can note that the order of the simulation is seemingly stuck at one (1). Furthermore, the simulation seems to be successful when the step size = 2.5E-05, but fails when a step of 5.0E-05 is attempted. The failure is always because of non-convergence of the corrector. You can also see that the Jacobian is evaluated automatically by DSTIFF.
A few strategies may be used to resolve the situation:- Investigate the modeling entities that cause the most error and try to remove any discontinuities and/or make the system "smoother" (forces, motions, stiffness, damping, and so on).
- Change the Jacobian evaluation pattern by increasing its evaluation frequency to help minimize corrector failures.
