MV-2050: Linear Analysis for Stability and Vibration Analysis
In this tutorial, you will learn how to perform a linear analysis using MotionView and MotionSolve. You will also learn how to interpret its results and use the same for improving the stability of your systems.
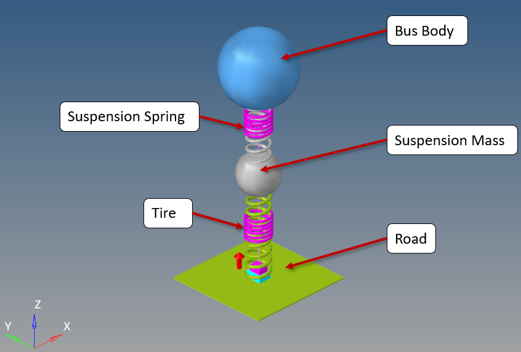
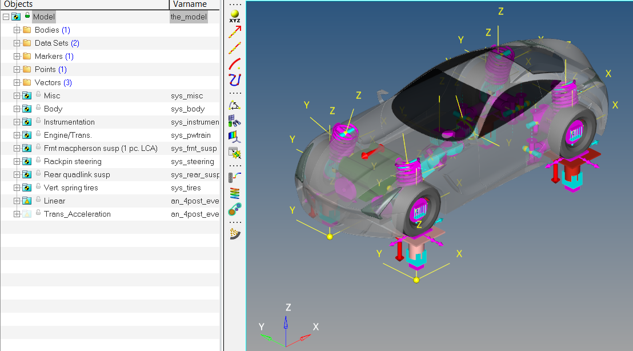
In this tutorial you will use a simplified quarter model of a bus represented by a two degrees of freedom system consisting of masses suspended by two springs. Next, you can optionally apply the concepts to perform a similar study using a real-life model of a full car provided here that makes some practical sense.
Open and Review the Simplified Quarter Bus Model
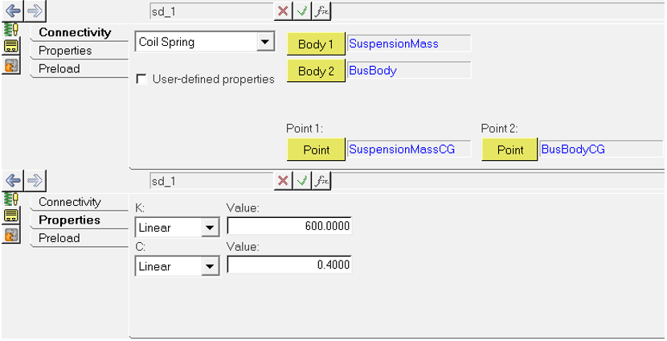
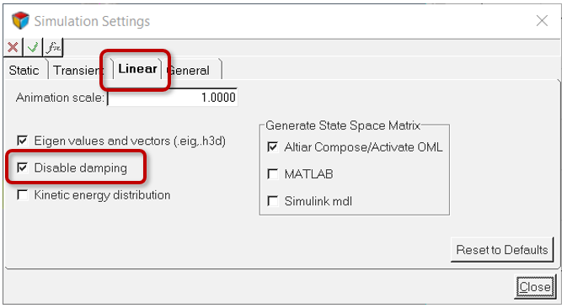
Determine Natural Frequencies
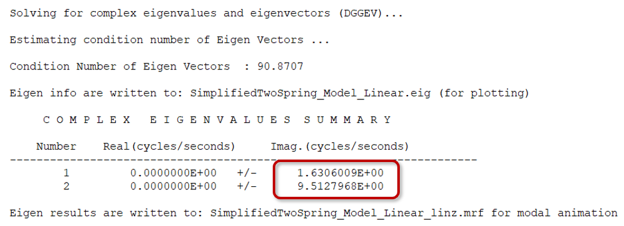
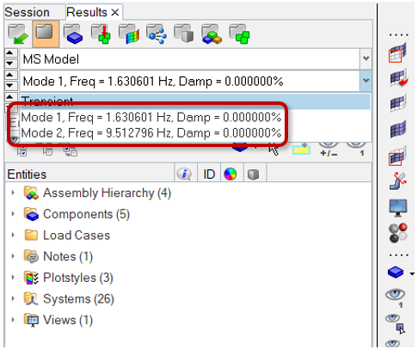
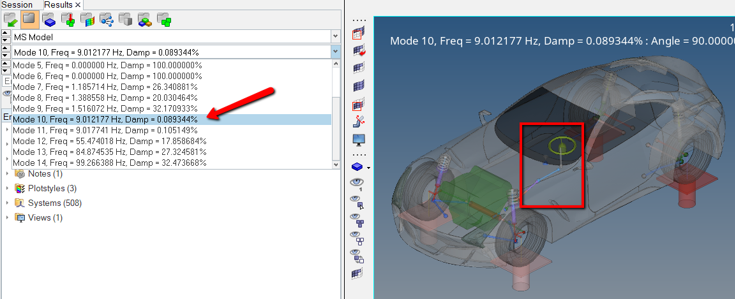
A linear analysis can be run on system to determine its natural frequencies and mode shapes.
Response to External Excitation
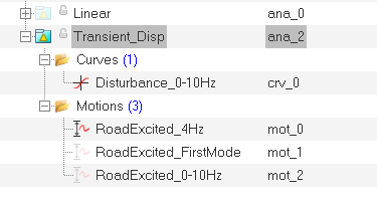
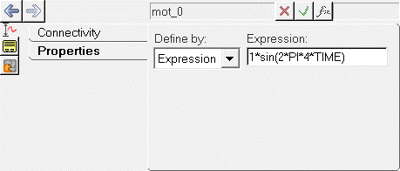
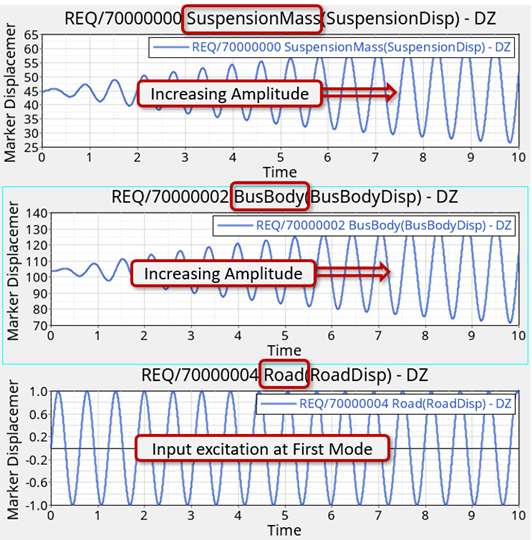
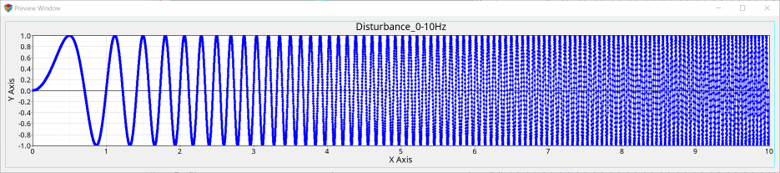
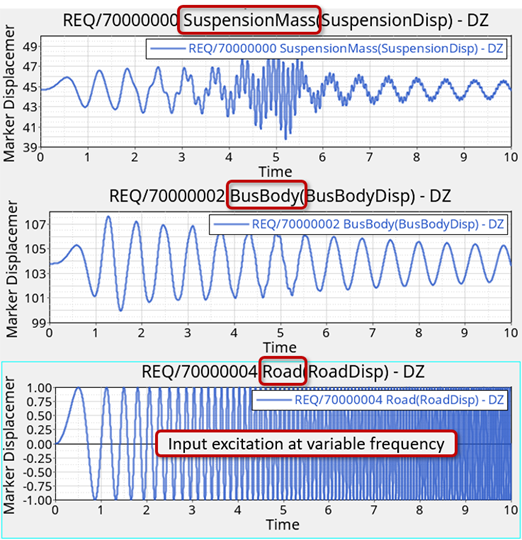
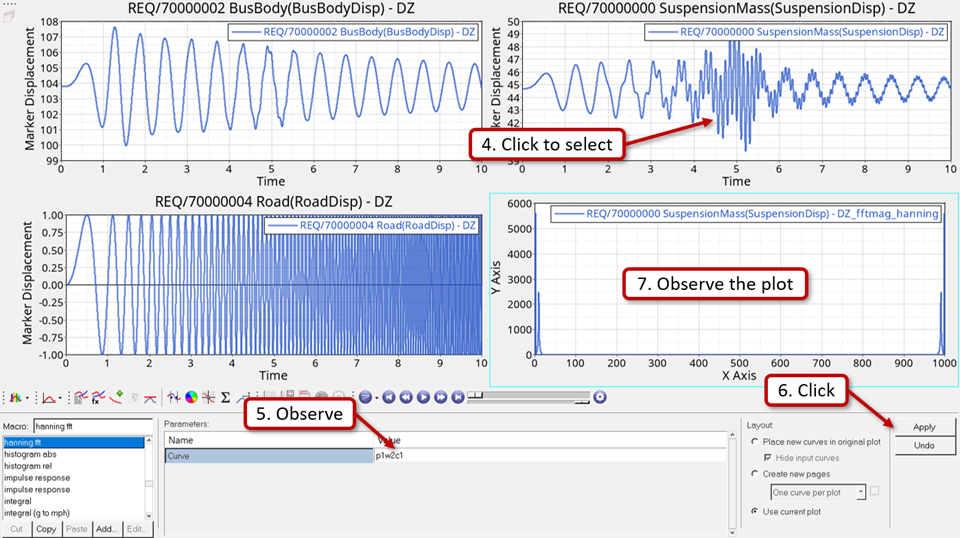
In this step a small enforced displacement in the form of a sinusoidal excitation on the road is applied at different frequencies to determine the response of the system. Here an expression of the form sin(2*π*f*t) is used, where ‘f’ is the natural frequency of the sine curve and ‘t’ is time.
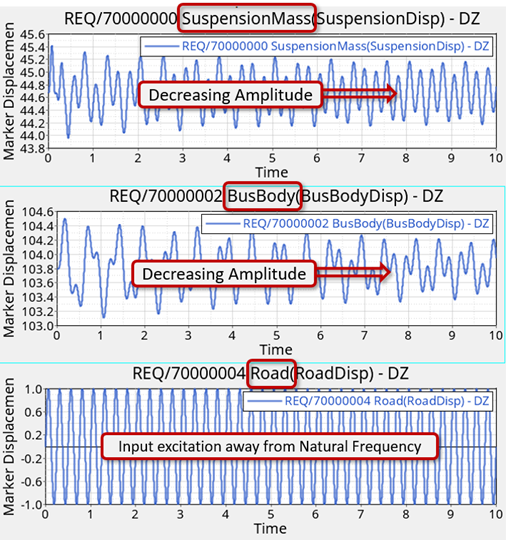
- Excitation at a frequency away from the natural frequency (in other words, 4Hz)
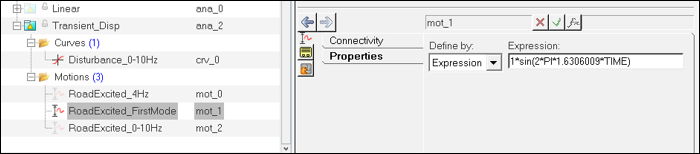
- Excitation at a natural frequency (in other words, First mode at ~ 1.63Hz)
- Excitation over a range of frequencies (from 0Hz to 10Hz)
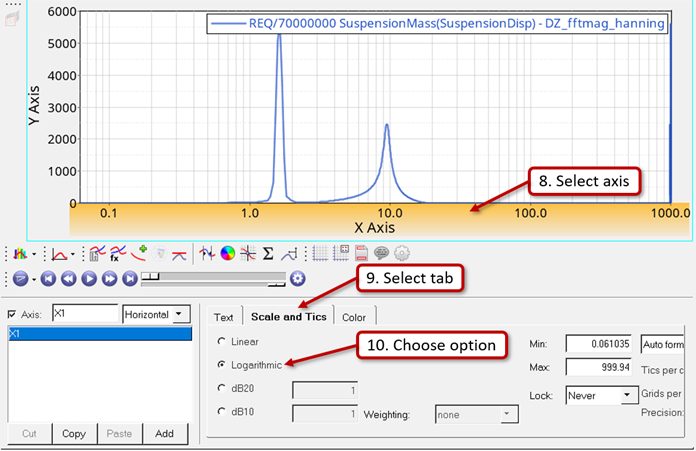
Convert Output to Frequency Domain
In this step the SuspensionMass displacement output plotted with respect to time will be used and plotted with respect to frequency using the Hanning type of Fourier Transforms.
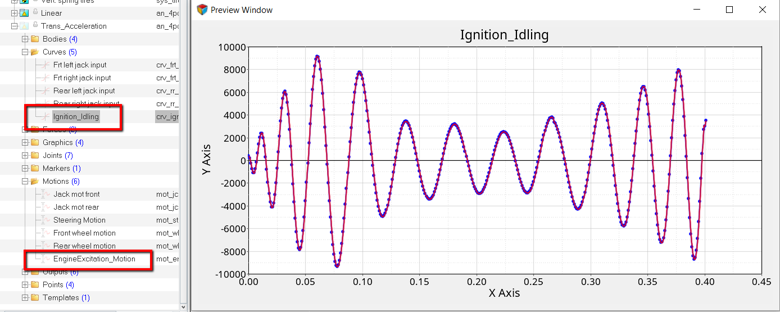
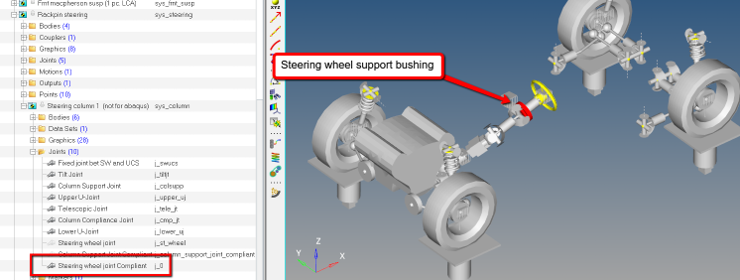
Study the Full Vehicle Model (optional)
A full car model has been provided with this tutorial as described earlier.