Flow Inside a Rotating Cavity

In this application, AcuSolve is used to simulate the flow of air in an enclosed cylindrical cavity with a rotating top and a fixed bottom. AcuSolve results are compared with experimental data adapted from Michelsen (1986). The close agreement of AcuSolve results with experimental data validates the ability of AcuSolve to model cases containing enclosed cavities with flow induced by rotating walls.

Problem Description

The problem consists of air in an enclosed cylinder 1.0 m tall with a radius of 1.0 m, as shown in the following image, which is not drawn to scale. The top of the cylinder rotates about its center at 1 rad/s, while the bottom of the cylinder is fixed. As the container top spins, the viscous stresses on the fluid induce a circumferential (swirl) velocity throughout the height of the cylinder. To conserve mass and momentum, the fluid generates a radial velocity that changes direction based on distance away from the rotation center of the cylinder.


Figure 1. Critical Dimensions and Parameters for Simulating Flow Inside a Rotating Cavity
The flow domain is modeled with axisymmetric periodicity in the circumferential direction, which allows for accurate simulation of the flow while minimizing computational time.


Figure 2. Mesh of Periodic Section Used for Simulating Flow Inside a Rotating Cylinder

AcuSolve Results

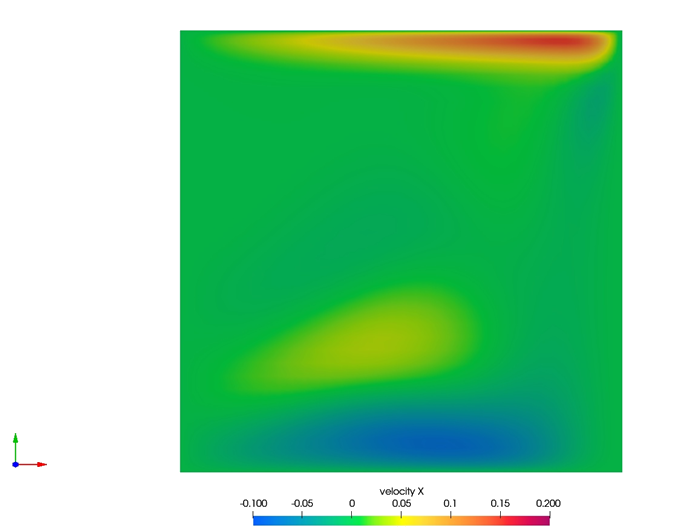
The AcuSolve solution converged to a steady state and the results reflect the mean flow conditions. The velocity varies with both vertical location and with distance from the rotation center. The complex flow field develops from a combination of the viscous stresses acting at the rotating cylinder top and at the stationary bottom.


Figure 3. Contours of Radial Velocity with Velocity Vectors. This Image Shows the Front Face of the Modeled Cylinder Wedge, with the Center of Rotation on the Left Edge. The Vertical Line Represents a Radial Location 0.6 m From the Center of Rotation.


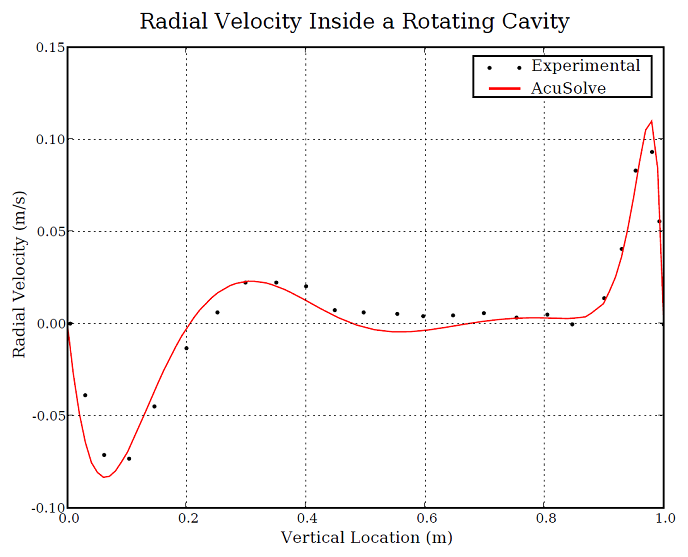
Figure 4. Radial Velocity (at 0.6 m From the Center of Rotation) as a Function of Vertical Location From Cylinder Bottom


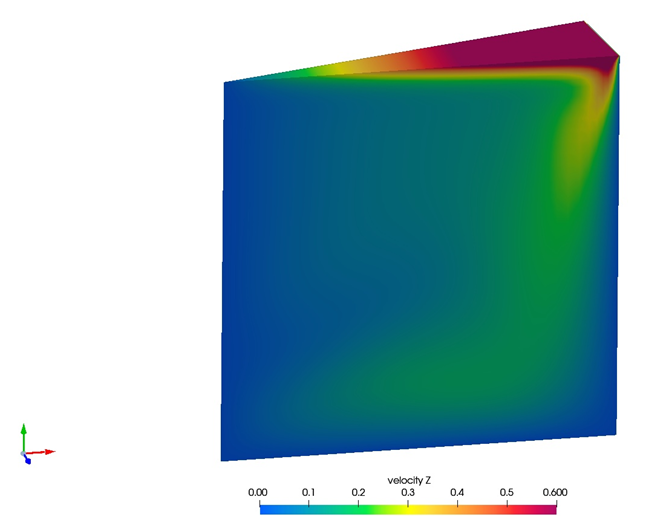
Figure 5. Contours of Swirl Velocity with Velocity Vectors


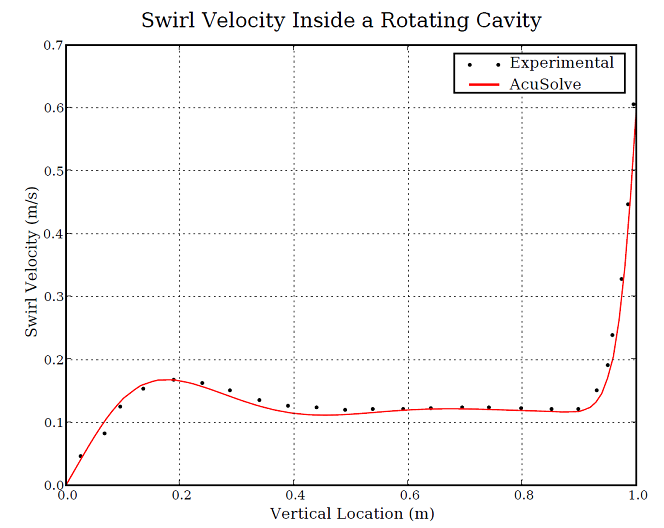
Figure 6. Swirl Velocity (at 0.6 m From Center of Rotation) as a Function of Vertical Location From the Cylinder Bottom

Summary

The AcuSolve solution compares well with the experimental data for flow induced by a rotating top of an enclosed cylinder. In this application, the flow in the fluid region is driven by the viscous stresses near the rotating top. Viscous stresses drag the fluid in a circular direction near the spinning wall. The angular velocity of the fluid decreases as distance from the top wall increases. Radial velocity develops as a result of the migration of the fluid toward the outer wall in regions of high angular velocity. The AcuSolve radial and swirl velocities compare very closely with the experimental data.

Simulation Settings for Flow Inside a Rotating Cavity

SimLab database file: <your working directory>\cavity_rotating\cavity_rotating.slb

Global

  • Problem Description
    • Solution type - Steady State
    • Flow - Laminar
  • Auto Solution Strategy
    • Relaxation Factor - 0.4
  • Material Model
    • Air
      • Density - 1.0 kg/m3
      • Viscosity - 0.000556 kg/m-sec
  • Reference Frame
    • Cavity Rotation
      • Rotation center
        • X-coordinate - 0.0
        • Y-coordinate - 0.0
        • Z-coordinate - 0.0
      • Angular velocity
        • X-component - 0.0
        • Y-component - -1.0 rad/sec
        • Z-component - 0.0

    Model

  • Volumes
    • Fluid
      • Element Set
        • Material model - Air
  • Surfaces
    • Bottom
      • Simple Boundary Condition
        • Type - Wall
    • Max_X
      • Simple Boundary Condition
        • Type - Wall
    • Max_Z
      • Simple Boundary Condition - (disabled to allow for periodic conditions to be set)
    • Min_Z
      • Simple Boundary Condition - (disabled to allow for periodic conditions to be set)
    • Top
      • Simple Boundary Condition
        • Type - Wall
        • Reference frame - Cavity Rotation
  • Periodics
    • Periodic 1
      • Periodic Boundary Condition
        • Type - Axisymmetric
        • Rotation axis
          • point 1
            • X-coordinate - 0.0 m
            • Y-coordinate - 0.0 m
            • Z-coordinate - 0.0 m
          • point 2
            • X-coordinate - 0.0 m
            • Y-coordinate - 1.0 m
            • Z-coordinate - 0.0 m

References

J. A. Michelsen. "Modeling of Laminar Incompressible Rotating Fluid Flow". AFM 86-05. Ph.D. thesis, Department of Fluid Mechanics, Technical University of Denmark. 1986.