OS-E: 3025 Optimization of the Modal Frequencies of a Disc using Constrained Beading Patterns

The problem posed by finding a good reinforcement pattern for four modal frequencies simultaneously is more than four times more difficult. Add to that the difficulty constraints on the variety of reinforcement patterns, and the problem becomes a formidable task.

Model Files

Refer to Access the Model Files to download the required model file(s).

Model Description

By implementing topography optimization and pattern grouping, the task is greatly simplified and good quality results are quickly generated. All optimization set up is done using the Optimization panel and its subpanels in HyperMesh.

The first four modal frequencies of a thin metal disc are to be optimized using bead reinforcement patterns. A variety of different manufacturing methods are being considered which place limitations on the bead reinforcement patterns allowed. The metal disc has a hole in the center where it is constrained (Figure 1).

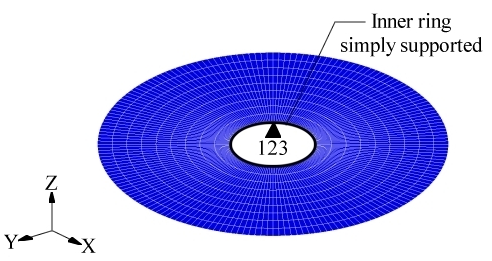
Figure 1. Constraints on the Disc Model

The objective for the model is to increase the sum of the frequencies of the first four normal modes of the disc. This is achieved by using the WFREQ response type. The WFREQ response is the sum of the inverse eigenvalues of the chosen frequencies. This is done in order to assign higher weight to the earlier modes than the latter ones.

The anchor node is set at the center of the disc and the first vector points in the z direction. The nodes in the center ring are removed from the design region by choosing Spc in the Boundary skip option in the topography subpanel. No other additions to the finite element model were required.

The solution for the circular reinforcement pattern method is shown in Figure 2. OptiStruct generated a single wide circular bead running from the inner ring to about three-quarters of the way to the outer edge of the disc. The bead is gently sloped throughout its width. This reinforcement pattern more than doubled the frequencies of the first three modes and increased the fourth and fifth modes by over 75%.

Figure 2. Solution for the Circular Bead Pattern Method

The solution for the radial reinforcement pattern is shown in Figure 3. OptiStruct generated a series of eight evenly spaced wide radial beads. Note that the beads are not drawn to their full height. This demonstrates that full height beads are not necessarily optimal. This reinforcement pattern also doubled the frequencies of the first three modes and increased the fourth and fifth frequencies by more than 70%, but was not quite as efficient as the circular pattern.

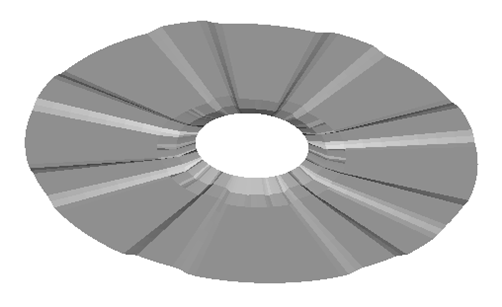
Figure 3. Solution for the Radial Bead Pattern Method

The solution for this setting is shown in Figure 4. OptiStruct generated a reinforcement pattern that appears to be a combination of the circular and radial reinforcement patterns. The inside of the disc has a series of radial beads while the outside has a roughly circular reinforcement. This reinforcement pattern had the best increases in the modal frequencies for all of the patterns compared.

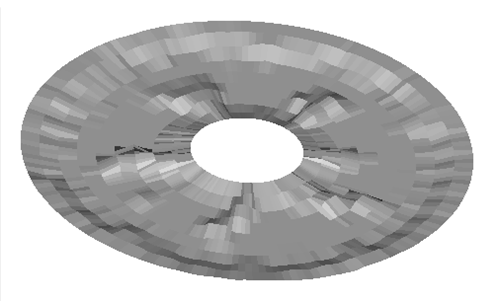
Figure 4. Solution for the Default Pattern Method

For cyclical symmetry, both the first vector (fields 12, 13, and 14) and second vector are defined in the same plane as the disc. The anchor node is located at the center of the disc. This cyclical pattern is set up to have four symmetric wedges with each wedge being symmetric about itself.

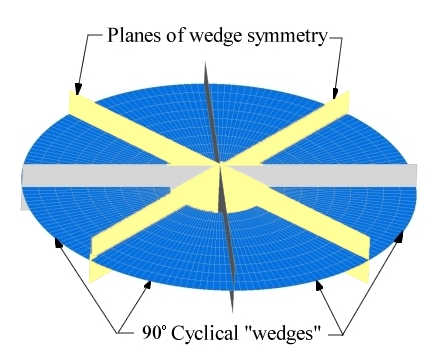
Figure 5. Cyclical Symmetry Pattern for 4 Symmetric Wedges

The solution for the cyclical pattern grouping option is shown in Figure 6. OptiStruct generated a reinforcement pattern very similar to the default pattern grouping pattern but with fourfold symmetry. The modal frequencies were slightly less than those for the default pattern.

Figure 6. Solution for the Cyclical Pattern Method with 4 Symmetric Wedges

Results