OS-E: 3010 Multi-plane Symmetric Reinforcement Optimization for a Pressure Vessel
A rectangular thin-walled box is to be used to store fluid. The outward bulging of the sides of the container (due to the pressure of the contents) is to be minimized. Additionally, the maximum outward displacement of the side panels must be below a given value.
Model Files
Refer to Access the Model Files to download the required model file(s).
- pressure.fem
- pressure13.fem
Model Description
The model is shown in Figure 1. All optimization set up is done using the optimization panel and its subpanels in HyperMesh.
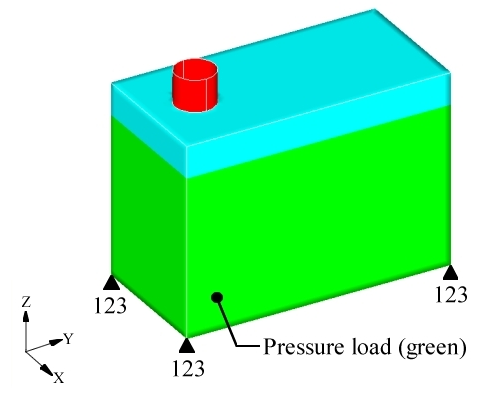
Figure 1. Loads and Constraints on Rectangular Pressure Vessel
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| DTPG | 1 | PSHELL | 1 | ||||||
| + | 7.0 | 60.0 | YES | 5.0 | NORM | NONE | |||
| + | PATRN | 30 | 50.0 | 100.0 | 75.0 | 0.0 | 1.0 | 0.0 | |
| + | PATRN2 | 0 | 0.0 | 0.0 | 1.0 | ||||
| + | BOUNDS | 0.0 | 1.0 |
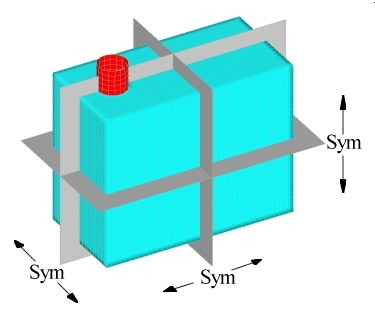
Figure 2. Orthogonal Symmetry Planes for the Pressure Box
The objective is to minimize compliance for the pressure load case, which is the same as minimizing the strain energy of the entire model. The displacement of the center point of each of the five loaded surfaces was constrained to be less than a given value.
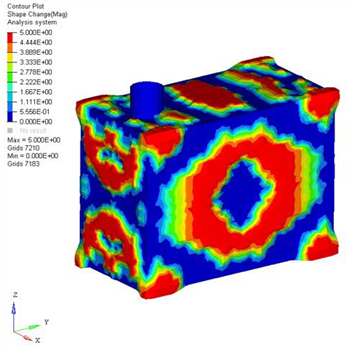
Figure 3. OptiStruct Solution for the Pressure Box
The OptiStruct solution met all of the optimization constraints and yielded a good design. The areas shown in red (Figure 3) are the bead reinforcements that OptiStruct created to increase the stiffness of the model. The solution is unconventional, but makes a good deal of engineering sense. For the large side panels and the top and bottom panels of the box, OptiStruct has generated large, rounded, centrally located reinforcement beads. These types of beads are very effective in stiffening the panels against a distributed or central load. This is due to the fact that bending in the central areas of the panels is occurring in two directions, both vertically and horizontally. The rounded beads create stiffness in both directions and are weak in neither. At the eight corners of the model, OptiStruct created beads that anchor the sides of the box together allowing each side of the box to gain support from the neighboring sides.

Figure 4. Finite Element Model of the OptiStruct Solution for the Pressure Box

Figure 5. Conventional Reinforcement Patterns for the Pressure Box
The OptiStruct model is superior in stiffness to both of the two conventional models. The maximum deflection of the OptiStruct model was 30% less than the lightly reinforced conventional model (the one on the left), and 46% less than the heavily reinforced model (the one on the right). The lightly reinforced model was stiffer than the heavily reinforced model, which goes against the assumption that more reinforcements result in increased stiffness. With bead type reinforcements that assumption is not always true, which demonstrates the effectiveness of topography optimization. OptiStruct delivers an optimized first design, eliminating the need to do a series of re-designs where the second, third, fourth, etc., model does not always result in an improvement.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| DTPG | 1 | PSHELL | 1 | ||||||
| + | 7.5 | 60.0 | YES | 5.0 | NORM | NONE | |||
| + | PATRN | 13 | 50.0 | 100.0 | 75.0 | 0.0 | 1.0 | 0.0 | |
| + | BOUNDS | 0.0 | 1.0 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| DTPG | 1 | PSHELL | 1 | ||||||
| + | 7.5 | 60.0 | YES | 5.0 | NORM | NONE | |||
| + | PATRN | 13 | 50.0 | 100.0 | 75.0 | 1.0 | 0.0 | 0.0 | |
| + | BOUNDS | 0.0 | 1.0 |
Results
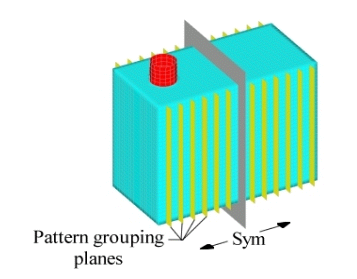
Figure 6. Planar Pattern Grouping Planes for Sides of Pressure Box
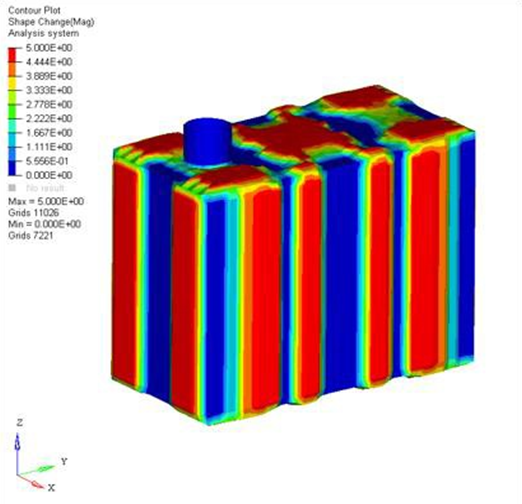
Figure 7. Pressure Box Solution for Combined Three-Plane and Planar Symmetry Options