/MONVOL/AIRBAG (Obsolete)

Format

Definitions

Comments

1. surf_ID_ex must be defined using segments associated with 4-nodes or 3-nodes shell elements (possibly void elements).
2. The volume must be closed and the normals must be oriented outwards.
3. Abscissa scale factors are used to transform abscissa units in airbag functions, for example:(1)
   $$\text{F}(\text{t}\prime )=\text{fct}\_\text{ID}\left(\frac{\text{t}}{{\text{Ascale}}_{\text{t}}}\right)$$

   Where, t is the time.

   For example, if your input data is in [ms], but you need a data in [s], you could set Ascale to 0.001.(2)

   $$\text{F}(\text{p}\prime )=\text{fct}\_\text{ID}\left(\frac{\text{p}}{{\text{Ascale}}_{\text{p}}}\right)$$

   Where, p is the pressure.

4. Initial pressure is set to P_ext.
5. Initial thermodynamic equilibrium is written at time zero (I_equi =0) or at beginning of jetting (I_equi =1), based on the following equation with respect to the volume at time zero, or the volume at beginning of jetting: ${\text{P}}_{\text{ext}}\text{V}=\text{R}\frac{{\text{M}}_0}{{\text{M}}_{\text{i}}}{\text{T}}_0$
   where, M₀ is the mass of gas initially filling the airbag, M_i is the molar mass of the gas initially filling the airbag, and R is the gas constant depending on the units system.(3)

   $$R=8.314\frac{\text{J}}{\mathit{mole}\cdot K}$$
6. Ratio of specific heats at constant pressure per mass unit cp_i of the gas initially filling the airbag is quadratic versus temperature:(4)
   $${\text{cp}}_{\text{i}}(\text{T})=\text{cpa}+{\text{cpb}}_{\text{i}}*\text{T}+{\text{cpc}}_{\text{i}}*{\text{T}}^2$$
7. Gas constant at initial temperature $\gamma$ _i must be related to specific heat per mass unit at initial temperature and molar mass of the gas initially filling the airbag with respect to the following relation:(5)
   $$\frac{(\gamma -1)}{{\gamma }_{\text{i}}}{\text{cp}}_{\text{i}}({\text{T}}_{\text{o}})=\frac{\text{R}}{{\text{M}}_{\text{i}}}$$
   Where, M_i is the molar mass of the gas initially filling the airbag, and R is the gas constant depending on the units system.(6)

   $$\text{R}=8.314\frac{\text{J}}{\text{mole}\cdot \text{K}}$$
8. The characteristics of the gas initially filling the airbag must be defined (no default) and must be equal for each communicating airbag.
9. If $\gamma$ _i = 0, the characteristics of the gas initially filling the airbag are set to the characteristics of the gas provided by the first injector.
10. Ratio of specific heats at constant pressure per mass unit cp_i of the gas is quadratic with regard to the temperature:(7)
    $$\text{cp}(\text{T})=\text{cpa}+\text{cpb}*\text{T}+\text{cpc}*{\text{T}}^2$$
11. Gas constant at initial temperature $\gamma$ must be related to specific heat per mass unit at initial temperature and molar mass of the with respect to the following relation:(8)
    $$\frac{(\gamma -1)}{\gamma }\text{cp}({\text{T}}_{\text{o}})=\frac{\text{R}}{\text{M}}$$
    Where,

    M

    Molar mass of the gas

    R

    Gas constant depending on the units system

    (9)

    $$\text{R}=8.314\frac{\text{J}}{\text{mole}\cdot \text{K}}$$
12. If jetting is used, an additional $\text{Δ}$ P_jet pressure is applied to each element of the airbag:(10)
    $$\Delta {\text{P}}_{\text{jet}}=\Delta \text{P}(\text{t})*\Delta \text{P}(\theta )*\Delta \text{P}(\delta )*\text{max}(\overrightarrow{n}*\overrightarrow{m},0)$$
13. With $\overrightarrow{m}$ being the normalized vector between the projection of the center of the element upon segment (node_ID₁ and node_ID₃) and the center of the element; $\theta$ the angle between vectors MN₂ and $\overrightarrow{m}$ (in degrees), $\delta$ is the distance between the center of the element and its projection upon segment (node_ID₁ and node_ID₃).
    The projection of a point upon segment (node_ID₁ and node_ID₃) is defined as the projection of the point in direction MN₂ upon the line (node_ID₁ and node_ID₃) if it lies inside the segment (node_ID₁ and node_ID₃). If this is not the case, the projection of the point upon segment (node_ID₁ and node_ID₃) is defined as the closest node node_ID₁ or node_ID₃.

    
    
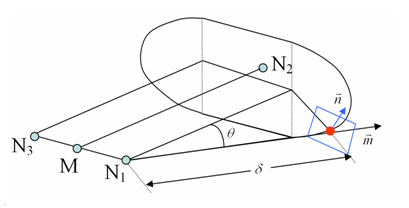
    Figure 1. Dihedral Shape of the Jet

    with M between N₁ and N₃

14. If node_ID₃ = 0, node_ID₃ is set to node_ID₁ and the dihedral shape is reduced to a conical shape.
15. If fct_ID_V = 0: isenthalpic outflow is assumed, else Chemkin model is used and outflow velocity is:(11)
    $$\nu ={\text{Fscale}}_{\text{V}}\ast \text{fct}\_{\text{ID}}_{\text{V}}\left(\text{P}-{\text{P}}_{\mathrm{ext}}\right)$$
    • Isenthalpic model

      Venting or the expulsion of gas from the volume, is assumed to be isenthalpic.

      The flow is also assumed to be unshocked, coming from a large reservoir and through a small orifice with effective surface area, A.

      Conservation of enthalpy leads to velocity, u, at the vent hole. The Bernouilli equation is then written as:

      (monitored volume) $\frac{\gamma }{\gamma -1}\frac{\text{P}}{\rho }=\frac{\gamma }{\gamma -1}\frac{{\text{P}}_{\text{ext}}}{{\rho }_{\text{vent}}}+\frac{{\text{u}}^2}{2}$ (vent hole)

      Applying the adiabatic conditions:

      (monitored volume) $\frac{\text{P}}{{\rho }^{\gamma }}=\frac{{\text{P}}_{\text{ext}}}{{{\rho }_{\text{vent}}}^{\gamma }}$ (vent hole)

      Where, P is the pressure of gas into the airbag and $\rho$ is the density of gas into the airbag.

      Therefore, the exit velocity is given by:(12)

      $${\text{u}}^2=\frac{2\gamma }{\gamma -1}\frac{\text{P}}{\rho }\left(1-{\left(\frac{{\text{P}}_{\text{ext}}}{\text{P}}\right)}^{\frac{\gamma -1}{\gamma }}\right)$$

      For supersonic flows the outlet velocity is determined as described in 10.4.4.1 of the Theory Manual.

      The mass out flow rate is given by:(13)

      $${\dot{\text{m}}}_{\text{out}}={\rho }_{\text{vent}}*\text{vent}\_\text{holes}\_\text{surface}*\text{u}=\rho {\left(\frac{{\text{P}}_{\text{ext}}}{\text{P}}\right)}^{\frac{1}{\gamma }}*\text{vent}\_\text{holes}\_\text{surface}*\text{u}$$
      The energy flow rate is given by:(14)

      $${\dot{\text{E}}}_{\text{out}}={\dot{\text{m}}}_{\text{out}}\frac{\text{E}}{\rho \text{V}}={\left(\frac{{\text{P}}_{\text{ext}}}{\text{P}}\right)}^{\frac{1}{\gamma }}*\text{vent}\_\text{holes}\_\text{surface}*\text{u}\frac{\text{E}}{\text{V}}$$

      Where, V is the airbag volume and E is the internal energy of gas into the airbag.

    • Chemkin model(15)
      $${\dot{\text{m}}}_{\text{out}}=\text{vent}\text{}\_\text{}\text{holes}\text{}\_\text{}\text{surface}*{\text{Fscale}}_{\text{v}}*\text{fct}\text{}\_\text{}{\text{ID}}_{\text{v}}\left(\text{P}-{\text{P}}_{\text{ext}}\right)*\rho$$

      Where, $\rho$ is the density of the gas within the airbag.

16. Vent holes surface is computed as follows:(16)
    $$\begin{array}{ll}\text{vent}\_\text{holes}\_\text{surface}\hfill & {\text{=A}}_{\text{vent}}*{\text{A}}_{\text{non}\_\text{impacted}}*\text{fct}\_{\text{ID}}_{\text{t}}({\text{A}}_{\text{non}\_\text{impacted}}/{\text{A}}_0)*\text{fct}\_{\text{ID}}_{\text{P}}(\text{P}-{\text{P}}_{\text{ext}})\hfill \end{array}$$
    (17)

    $$\begin{array}{l}+{\text{B}}_{\text{vent}}*{\text{A}}_{\text{impacted}}*\text{fct}\_{\text{ID}}_{{\text{t}}^{\prime }}({\text{A}}_{\text{impacted}}/{\text{A}}_0)*\text{fct}\_{\text{ID}}_{{\text{P}}^{\prime }}(\text{P}-{\text{P}}_{\text{ext}})\hfill \end{array}$$
    with impacted surface:(18)

    $${\text{A}}_{\text{impacted}}=\sum _{\text{e}\in {\text{S}}_{\text{vent}}}\frac{{\text{n}}_{\text{c}}\left(\text{e}\right)}{\text{n}\left(\text{e}\right)}{\text{A}}_{\text{e}}$$
    and non-impacted surface:(19)

    $${\text{A}}_{\text{non}\_\text{impacted}}=\sum _{\text{e}\in {\text{S}}_{\text{vent}}}\left(1-\frac{{\text{n}}_{\text{c}}\left(\text{e}\right)}{\text{n}\left(\text{e}\right)}\right){\text{A}}_{\text{e}}$$

    Where for each element e of the vent holes surf_ID_v, n_c(e) means the number of impacted nodes among the n(e) nodes defining the element.

    
    
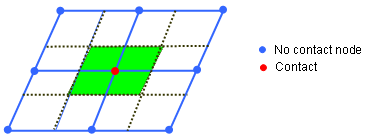
    Figure 2. From Nodes Contact to Impacted/Non-impacted Surface

17. Functions fct_ID_t' and fct_ID_P' are assumed to be equal to 1, if they are not specified (null identifier).
18. Function fct_ID_A' is assumed as the fct_ID_A'(A) = A, if it is not specified.
19. In order to use porosity during contact, flag I_BAG must be set to 1 in the interfaces concerned (Line 3 of interface Type 5 and Type 7). If not, the nodes impacted into the interface are not considered as impacted nodes in the previous formula for A_impacted and A_{non_impacted}.
20. When defining venting, there are some limitations concerning the definition of airbag surface and surface venting:
    • The airbag external surface should be built only from shells and 3-nodes shell elements.
    • The airbag external surface can not be defined with option /SURF/SEG (or with option /SURF/SURF if a sub-surface is defined with option /SURF/SEG).
    • Same restriction applies to vent hole surface.
    • Shells and 3-nodes shell elements included in vent hole surface have to also be included in external surface.
21. Vent hole membrane is deflated if T > T_vent or if the pressure exceeds P_def during more than $\text{Δt}{P}_{def}$ .