/PROP/TYPE26 (SPR_TAB)
Block Format Keyword Defines the tabulated spring property.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /PROP/TYPE26/prop_ID/unit_ID or /PROP/SPR_TAB/prop_ID/unit_ID | |||||||||
| prop_title | |||||||||
| M | sens_ID | Isflag | Ileng | ||||||
| Nfunc | Nfund | Lscale | Kmax | Dmax | Alpha | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_ID1 | Fscale | Strain_rate | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_ID1 | Fscale | Strain_rate | |||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| prop_ID | Property
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| prop_title | Property
title. (Character, maximum 100 characters) |
|
| M | Mass. 2 (Real) |
|
| sens_ID | Sensor
identifier. (Integer) |
|
| Isflag | Sensor flag. 3
(Integer) |
|
| Ileng | Input per unit length
flag. 2
(Integer) |
|
| Nfunc | Numbers of loading
curves. (Integer) |
|
| Nfund | Numbers of unloading
curves. (Integer) |
|
| Lscale | Scale factor for abscissa
of loading and unloading functions depending on flag Ileng. 6 Default = 1 (Real) |
|
| Kmax | Maximum
stiffness. (Real) |
|
| Dmax | Failure
displacement. (Real) |
|
| Alpha | Strain rate filtering
factor. Values between 0.0 and 1.0. Default value = 1.0 (no strain filtering) (Real) |
|
| fct_ID1 | Function identifier
defining f(
) or f(
) depending on flag Ileng. (Integer) |
|
| Fscale | Scale factor for loading
and unloading functions. (Real) |
|
| Strain_rate | Displacement or strain
rate depending on Ileng which corresponds to a loading or unloading
function. (Real) |
Comments
- Let = L - be the difference between the current length and the initial length of the spring element.
- If Ileng=1, the spring properties are based on the reference
spring length. The input should be entered as: Each spring will then have the following properties in the model:Where,
- and
- Spring values entered in the spring property fields
- and
- Spring’s actual physical mass, stiffness and damping
- Initial spring length which is the distance between node N1 and N2 of the spring
- Dmax
- Entered as engineering strain
- Strain_rate
- Entered as engineering strain rate
- Spring is activated
and/or deactivated by sensor defined in sens_ID and depends on Isflag:
- If Isflag = 0, the spring element is activated by the sens_ID and cannot be deactivated. The initial length of the spring is based on the spring length at time=0.
- If Isflag = 1, the spring element is deactivated by the sens_ID and cannot be activated. The initial length of the spring is based on the spring length at time=0.
- If Isflag = 2, the spring is activated and/or deactivated by sens_ID and can switch activation state multiple times. If sensor is activated, the spring is active; if sensor is deactivated, spring is deactivated. The spring initial length, , is the distance between spring nodes at the time of sensor activation.
- Force calculations:
- If Ileng =0, the force is defined as a function of
displacement:
(1) - If Ileng =1, the force is defined as a function of
strain:
(2)
Where,- Engineering strain.
- Reference length of the element, with
- If Ileng =0, the force is defined as a function of
displacement:
- Spring forces are
calculated using loading and unloading functions for different rates.
- The rate is determined and the maximum loading force as well as the minimum unloading force is determined by interpolation from the input curves.
- The behavior between the loading and unloading curves is linear, using Kmax value as the spring stiffness.
- For both loading and unloading, input curves should be defined in order of strictly increasing strain rate values.
- To describe spring compression behavior, input curves Force(strain) should be strictly positive.
- In traction, spring behavior is linear with stiffness equal to
Kmax.
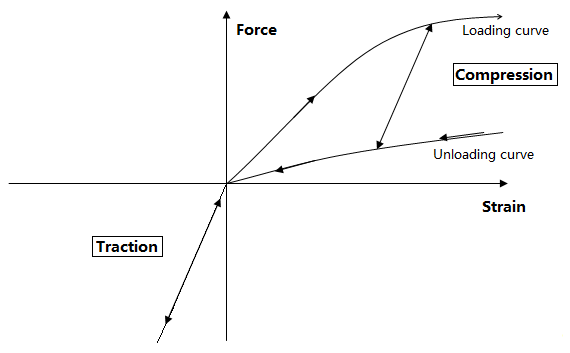
Figure 1.
Figure 2.
- Lscale is used only when the Ileng =0 (abscissa unit is length); otherwise the default value =
1.
(3) Where, is the function of fct_ID1.