/PROP/TYPE27 (SPR_BDAMP)
Block Format Keyword Describes a damper spring property with one translational DOF. Damper force is bounded by stiffness force.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /PROP/TYPE27/prop_ID/unit_ID or /PROP/SPR_BDAMP/prop_ID/unit_ID | |||||||||
| prop_title | |||||||||
| Mass | sens_ID | Isflag | Ileng | Itens | Ifail | ||||
| K | C | n | |||||||
| gap | Fsmooth | Fcut | |||||||
| fct_ID1 | fct_ID2 | Ascale1 | Fscale1 | Ascale2 | Fscale2 | ||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| prop_ID | Property identifier. (Integer, maximum 10 digits) |
|
| unit_ID | (Optional) Unit Identifier. (Integer, maximum 10 digits) |
|
| prop_title | Property title. (Character, maximum 100 characters) |
|
| Mass | Mass. (Real) |
(Ileng = 0) (Ileng = 1) |
| sens_ID | Sensor identifier.
(Integer) |
|
| Isflag | Sensor flag.
(Integer) |
|
| Ileng | Input per unit length flag.
(Integer) |
|
| Itens | Tensile behavior flag.
(Integer) |
|
| Ifail | Failure model flag.
(Integer) |
|
| K | Linear loading and unloading
stiffness. (Real) |
(Ileng = 0) (Ileng = 1) |
| C | Linear damping
coefficient. Default = 0.0 (Real) |
(Ileng = 0) (Ileng = 1) |
| n | Exponent for nonlinear stiffness
force. Default = 1.0 (Real) |
|
| Negative failure limit. Default = -1020 (Real) |
||
| Ifail = 1: Failure displacement (Ileng = 0) Failure strain (Ileng = 1) |
(Ileng = 0) | |
| Ifail = 2: Failure force. | ||
| Positive failure limit. Default = 1020 (Real) |
||
| Ifail = 1: Failure displacement (Ileng = 0) Failure strain (Ileng = 1) |
(Ileng = 0) | |
| Ifail = 2: Failure force. | ||
| gap | Minimum gap before
activation. Default = 0.0 (Real) |
(Ileng = 0) |
| Fsmooth | Spring force filtering flag.
(Integer) |
|
| Fcut | Cutoff frequency for spring force
filtering. Default = 100 kHz (Real) |
|
| fct_ID1 | Nonlinear stiffness force function
identifier:
(Integer) |
|
| fct_ID2 | Damping force function identifier:
(Integer) |
|
| Ascale1 |
Default = 1.0 (Real) |
(Ileng = 0) |
| Fscale1 | Ordinate scale factor for the
stiffness function
. Default = 1.0 (Real) |
|
| Ascale2 |
Default = 1.0 (Real) |
(Ileng = 0) (Ileng = 1) |
| Fscale2 | Ordinate scale factor for the
stiffness function
. Default = 1.0 (Real) |
Comments
- The spring has one translational degree of freedom in the local x direction which is defined between node N1 and N2 of the spring.
- Force
computation is activated by default in compression (
< 0), and in tension only if
Itens = 1. The
spring force value is obtained as follows, where Ileng = 0:
- Stiffness part:
Where, .
- Damping
part:
- Global
force:
- Stiffness part:
- If the Ileng flag is activated (Ileng = 1), the above computations become:
- Stiffness part:
- Damping part:
- Global force:
- Stiffness part:
- You can define a
compression gap activation as defined on the following scheme:
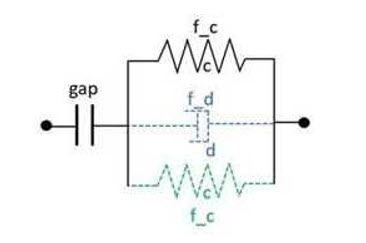
Figure 1.If the gap is defined (gap ≠ 0.0) the force computation is activated once the spring compression is bigger than the specified gap.(1) Note: Defining a gap value implies that the spring only works in compression and thus, Itens = 0, if the gap is defined. If Ileng = 1, the gap is homogeneous to a compressive strain. - The switching
between the two forces computation’s formula can lead to a noisy spring
response. To address this issue, you can use filtering on the spring force
computation, allowing a smooth transition between the two spring states
(damped and undamped). To do so, the force filtering flag Fsmooth and the cutoff frequency Fcut can be used as:
- If Fcut ≠ 0.0, the filtering is activated (Fsmooth is automatically set to 1), and the filtering uses the cutoff frequency provided by you.
- If Fsmooth =1 and Fcut = 0.0, the filtering is activated and a default cutoff frequency of 100 kHz is used.
- If Fsmooth =0 and Fcut = 0.0, no filtering is used.
If the filtering is activated, the spring force is computed as:(2) Where,