Spring Joint TYPE45 (/PROP/KJOINT2)
In Radioss, property TYPE45 is the joint type spring.
DOF of KJOINT2
The DOF (degrees of freedom) of KJOINT2 are defined with option “Type.” Different types of joint made by different DOF combinations. The following types are available in Radioss:
| Type No. | Joint Type | dx | dy | dz | x | y | z |
|---|---|---|---|---|---|---|---|
| 1 | Spherical | x | x | x | 0 | 0 | 0 |
| 5 | Universal (development source only) | x | x | x | x | 0 | 0 |
| 2 | Revolute | x | x | x | 0 | x | x |
x: denotes a fixed degree of freedom
0: denotes a free (user-defined) degree of freedom
| Type No. | Joint Type | dx | dy | dz | x | y | z |
|---|---|---|---|---|---|---|---|
| 6 | Translational | 0 | x | x | x | x | x |
| 6 | Oldham | x | 0 | 0 | x | x | x |
x: denotes a fixed degree of freedom
0: denotes a free (user-defined) degree of freedom
| Type No. | Joint Type | dx | dy | dz | x | y | z |
|---|---|---|---|---|---|---|---|
| 3 | Cylindrical | 0 | x | x | 0 | x | x |
| 4 | Planar | x | 0 | 0 | 0 | x | x |
x: denotes a fixed degree of freedom
0: denotes a free (user-defined) degree of freedom
| Type No. | Joint Type | dx | dy | dz | x | y | z |
|---|---|---|---|---|---|---|---|
| 8 | Rigid | x | x | x | x | x | x |
| 9 | Free | 0 | 0 | 0 | 0 | 0 | 0 |
x: denotes a fixed degree of freedom
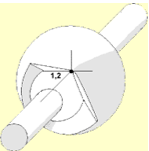 Figure 1. Spherical |
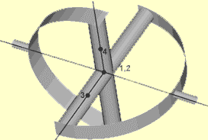 Figure 2. Universal |
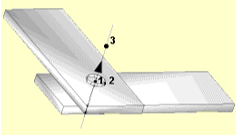 Figure 3. Revolute |
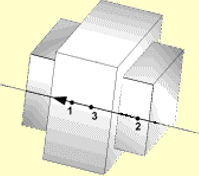 Figure 4. Translational |
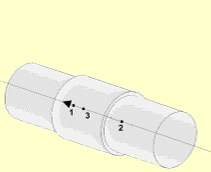 Figure 5. Cylindrical |
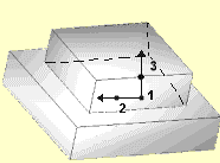 Figure 6. Planar |
The coordinate for DOF is the one used for spring force computation. It is not necessarily the spring local coordinate system. Depending on the different types of KJOINT2 and the definition of skew, different coordinate systems are used for spring force computations.
Stiffness and Damping in KJOINT2
- Blocked stiffness
. For example, for blocked stiffness =
Yes:
- If Type = 1 (Spherical), then are blocked stiffnesses in translational directions .
- If Type = 6 (Translational), then
are blocked stiffnesses in
translational directions
and in rotational directions
.
Table 7. Type No. Joint Type dx dy dz x y z 1 Spherical x x x 0 0 0 6 Translational 0 x x x x x If = 0 (default), Radioss computes blocked stiffness internally. If > 0, user-defined blocked stiffness is used.
- Translational stiffness
and rotational stiffness
. These stiffnesses are used in free DOF
direction and used for force and moment computation:
Table 8. Linear Spring Nonlinear Spring : translational stiffness
: rotational stiffness
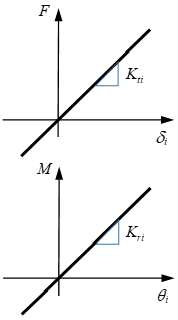
Figure 7.: translational stiffness factor
: rotational stiffness factor
is translational stiffness function fct_
is rotational stiffness function fct_
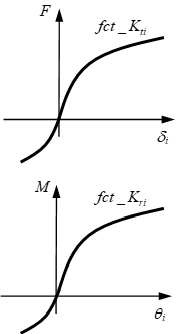
Figure 8. - Translational viscosity coefficient
and rotational viscosity coefficient
are for damping. These viscosity
coefficients are used in free DOF direction and used for force and moment
computation.
Table 9. Linear Spring Nonlinear Spring : translational stiffness
: rotational stiffness
: translational stiffness factor
: rotational stiffness factor
is translational stiffness function fct_
is rotational stiffness function fct_
For example, tensile spring (which used KJOINT2) with constant velocity = 1.33:- If only translational stiffness is set to , then force (green curve in figure below) increases with .
- If only translational viscosity is set to , then force (orange curve in figure below) is constant since tensile velocity is constant. The force is .
- If both translational stiffness
and translational viscosity
are set, then force (blue curve
in figure below) is the combination of the above two cases with
.
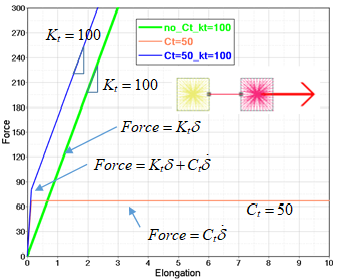
Figure 9.
- Frictional stiffness in translational direction
and in rotational direction
. These are used to compute penalty force to
prevent displacement exceeding the limit
or rotation exceeding the limit
.
If are not set, Radioss will compute it automatically with very high stiffness.
For example, in the following tensile test, setting , then:- If are not set (figure below on the left), then very high stiffness is used after reaching limit .
- If
is set (figure below on the
right), then
is used after reaching limit
.

Figure 10.The above tests also show translational stiffness . This only affects force before reaching the limit . The value of should not be set too small. This value is used to simulate blocking behavior after reaching the limit. Too small a value for leads to the following error message:WARNING ID : 979 ** WARNING IN FRICTION DEFINITION FOR KJOINT2 DESCRIPTION : ELASTIC STIFFNESS 0.1000000000000 IS SMALLER THAN THE MAX DERIVATIVE 720.0000000000 OF THE FRICTION FUNCTION 0
- If is not set but . The figure below on the left shows how constant friction force affects the spring force. With , force increases with to 15,000 and then remains constant until reaching the limit . After reaching , force increases with stiffness again.
- If, as in the previous case, an additionally set translation
stiffness
(figure below on the right),
then force increases with
to
and then increases with
translation stiffness
until reaching the limit
. After reaching
, force increases with stiffness
again.
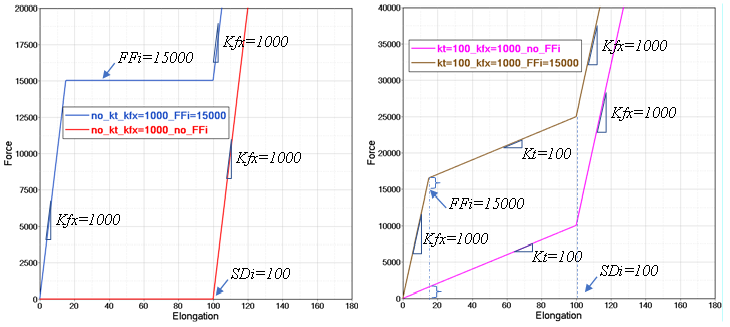
Figure 11.must be defined if it is required to consider friction behavior after reaching the stop limit. Otherwise, even if friction (constant friction or friction curve ) has been defined, Radioss will still take the internally computed (very high) stiffness to treat the force (or moment) behavior after reaching the limit.