Verification Manual

Introduction

Two implementations of MotionSolve’s journal bearings, a Dynamic Gumbel Long Aligned Journal Bearing and a Gumbel Short Misaligned Journal Bearing, are verified by comparing their behavior against data found in 1 and 2. The purpose of the verification is to establish the truth, accuracy, and validity of the journal bearing elements in MotionSolve.

Test Subject - Aligned Journal Bearing

The journal mass is equal to 0.13 kg and its polar moment of inertia is 250 kg*mm^2. The bearing is fixed to the ground, while the journal is rotating at a constant angular velocity of ω=500 rpm. Additionally, an external constant vertical load equal to F=30 N is applied at the journal’s center, as depicted in Figure 1.

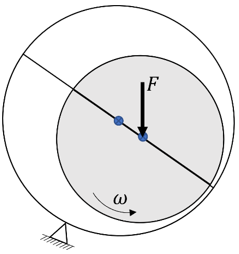
Figure 1. Schematic Diagram of the Aligned Journal Bearing

Diagram 1 compares the journal’s center orbit between MotionSolve and 1. The external load is parallel to the diagram’s vertical axis.

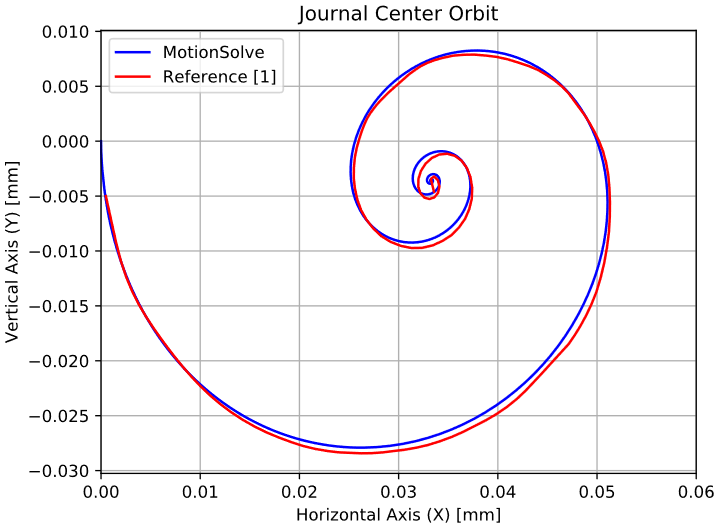
Figure 2. Diagram 1 - Journal Center Orbit

There is a very good correlation between MotionSolve and the curves provided by 1. Due to the constant external load, the journal follows a spiral orbit until it reaches a steady state.

Diagrams 2 and 3 present the horizontal (Fx) the vertical (Fy) lubrication forces with respect to time. These are total hydrodynamic forces acting on the journal. Forces calculated by MotionSolve in both directions are almost identical to the respective forces in 1.

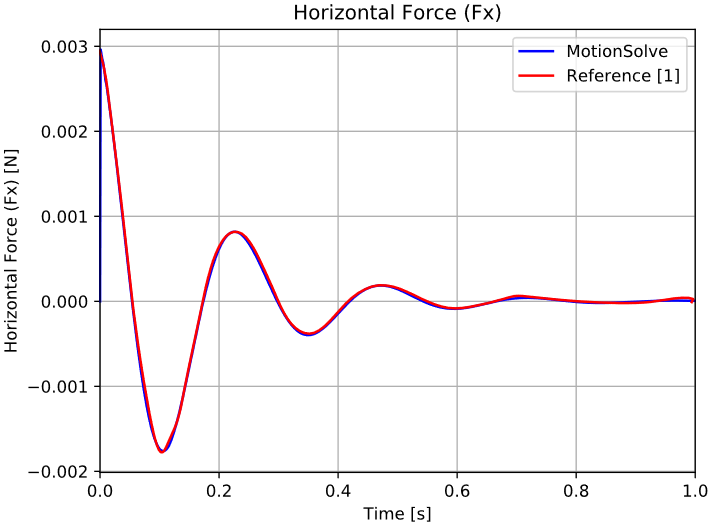
Figure 3. Diagram 2 - Horizontal Lubrication Force (Fx)

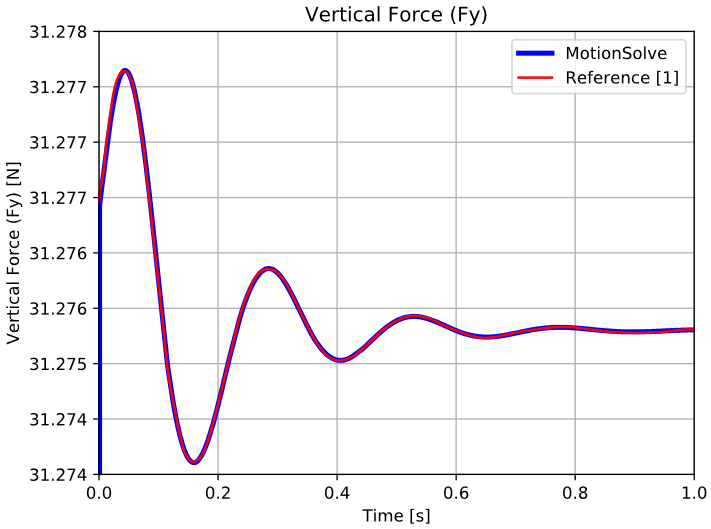
Figure 4. Diagram 3 - Vertical Lubrication Force (Fy)

Those oscillating forces decay with time due to the damping characteristics of the fluid until they reach steady value. In this steady state condition, the horizontal force is zero since no external load in the horizontal direction is applied, while the vertical force is the sum of the journal weight and the external load.

Test Subject - Misaligned Journal Bearing

In the second test subject, an unbalanced rotor supported by two Misaligned Journal Bearings 2 is simulated. Cavitation is considered, so negative pressures are not taken into consideration. Thus, the method that is used for the two misaligned journal bearings is the Gumbel Short. In the following figure, the rotor and journal bearings assembly are depicted.

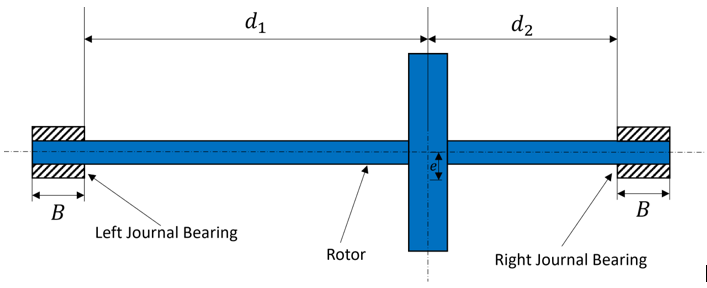
Figure 5. Schematic Diagram of the Unbalanced Rotor

Diagram 4 compares the journal center orbit of the left journal bearing between MotionSolve and 2.

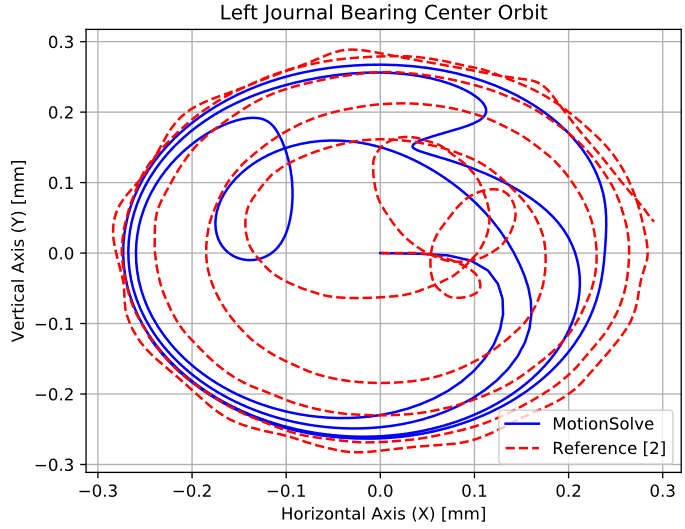
Figure 6. Diagram 4 - Left Journal Bearing Center Orbit

The comparison does not show any similarities between MotionSolve and 2 during the initial transient phase, but converges to a good correlation once steady state is achieved. In steady state, the two orbits are very similar.

In contrast to ideal rigid bearings (for example, a revolute joint), journal bearings provoke an elliptical orbit since they act more like spring-dampers than a perfect joint. Thus, the dynamics of the system are more complicated.

Time histograms of lubrication forces cannot be compared due to the lack of such data in 2.

Conclusion

Comparisons of MotionSolve journal bearing models against literature models were conducted. The comparison was first performed on a Dynamic Gumbel Long Aligned Journal Bearing, followed by a Gumbel Short Misaligned Journal Bearing. In the simple aligned journal bearing model, the correlation between the models is almost perfect. Only very small deviations exist. In the more complicated model of the rotor, good correlation is approached at steady state. The verification was performed only on two types of journal bearings, while the library includes more of them. The remaining journal bearing types use the same principles and a similar outcome as shown here can be expected.

References