/FRAME/MOV2

Block Format Keyword Describes moving frames. Relative motion with respect to a reference frame. Moving frame definition differs from /FRAME/MOV. 8

Format

(1)	(2)	(3)
/FRAME/MOV2/`frame_ID`
`frame_title`
`node_ID`₁	`node_ID`₂	`node_ID`₃

Definition

Field	Contents	SI Unit Example
`frame_ID`	Reference frame identifier - must be different from all skew identifiers. (Integer, maximum 10 digits)
`frame_title`	Reference frame title (Character, maximum 100 characters)
`node_ID`₁	Node identifier `N`₁ (Integer)
`node_ID`₂	Node identifier `N`₂ (Integer)
`node_ID`₃	Node identifier `N`₃ (Integer)

Comments

Let a moving reference frame $Λ_{t} (A, u, v, w)$ $Λ_{t} (A, u, v, w)$ .
For each time t, the frame position and orientation are determined via its original position $x_{A}$ $x_{A}$ and a rotation (orientation) matrix $R$ $R$ .
Let $w$ $w$ be the instantaneous rotational velocity of $λ$ $λ$ .
For each time t, the local coordinates of $x_{l}$ $x_{l}$ a point M with respect to the frame are related to its coordinates $x_{G}$ $x_{G}$ into the global system, as:(1)
$x_{G} = x_{A} + R x_{l}$ $x_{G} = x_{A} + R x_{l}$
The relative displacement $u_{l} = x_{l} - x_{l}^{0}$ $u_{l} = x_{l} - x_{l}^{0}$ of M between time 0 and t, with respect to the frame is related to its displacement with regard to the global system, as:(2)
$u_{G} = u_{A} + (R - R^{0}) x_{l} + R u_{l}$ $u_{G} = u_{A} + (R - R^{0}) x_{l} + R u_{l}$
The relative velocity of M with respect to the frame is related to its velocity with regard to the global system, as:(3)
$R v_{l} = v_{G} - v_{e}$ $R v_{l} = v_{G} - v_{e}$

Where, $v_{e} = v_{A} + ω \times A M$ $v_{e} = v_{A} + ω \times A M$ is the driving velocity; that is the velocity of the point coincident with M at time t and fixed with respect to the reference frame.
The relative acceleration of M with respect to the frame M is related to its acceleration with regard to the global system, as:
(4)
$R γ_{l} = γ_{G} - γ_{e} - γ_{c}$ $R γ_{l} = γ_{G} - γ_{e} - γ_{c}$

Where,

$γ_{e} = γ_{A} + \frac{d ω}{d t} \times A M + ω \times (ω \times A M)$ $γ_{e} = γ_{A} + \frac{d ω}{d t} \times A M + ω \times (ω \times A M)$

Driving acceleration

$γ_{c} = 2 ω \times v_{r e l a t i v e}$ $γ_{c} = 2 ω \times v_{r e l a t i v e}$

Acceleration, due to Coriolis forces
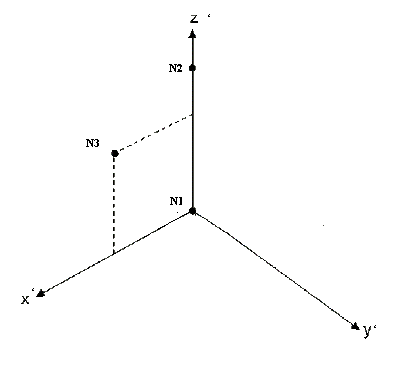
For a moving reference frame, the reference frame position and orientation vary with time and are defined by N₁, N₂ and N₃.
The origin of the frame is defined by the position of N₁.

node_ID₁and node_ID₂ define $Z^{'}$

node_ID₁ and node_ID₃ define $X "$ (5)
$Y' = Z^{'} Λ X "$
(6)
$X' = Y' Λ Z'$

Figure 1.

Reference frame identifier must be different from all skew identifiers.