/MAT/LAW10 (DPRAG1)

The yield criteria is pressure dependent. To compute the pressure an equation of state must be provided (such as /EOS/COMPACTION). This law is compatible only with solid elements.

Important: Starting in version 2019.1, the equation of state (EOS) parameters were removed from this material law. Any model using the old format that includes the EOS parameters will be converted during import into the updated material law format with an associated /EOS/COMPACTION.

Format

(1)	(3)	(5)	(7)
/MAT/LAW10/`mat_ID`/`unit_ID` or /MAT/DPRAG1/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$ν$
`A`₀	`A`₁	`A`₂	`A`_max
$Δ P_{\min}$

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
`E`	Young's modulus. (Real)	$[Pa]$
$ν$	Poisson's ratio. (Real)
`A`₀	Yield criteria coefficient. (Real)	$[P a^{2}]$
`A`₁	Yield criteria coefficient. (Real)	$[Pa]$
`A`₂	Yield criteria coefficient. (Real)
`A`_max	Yield criteria limit (von Mises limit). (Real)	$[P a^{2}]$
$Δ P_{\min}$	Minimum pressure. Default = -10³⁰ (Real)	$[Pa]$

▸Example (Concrete)

#RADIOSS STARTER
/UNIT/1
unit for mat
                   g                  cm                 mus
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW10/1/1
Concrete
#              RHO_I
                 2.4                   
#                  E                  Nu
                .576                 .25
#                 A0                  A1                  A2                Amax
            9.72E-10             4.32E-5                 .48                .013
#              P_min 
              -1E-20 
/EOS/COMPACTION/1/1
Concrete EOS
#                 C0                  C1                  C2                  C3
                 0.0               0.256               0.256                   1
#              MUMIN               MUMAX                BUNL
                 0.0                0.44               0.115
#                PSH                RHO0
                   0                2.40  
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA

Comments

Original Drucker-Prager yield criterion has a linear pressure dependency.

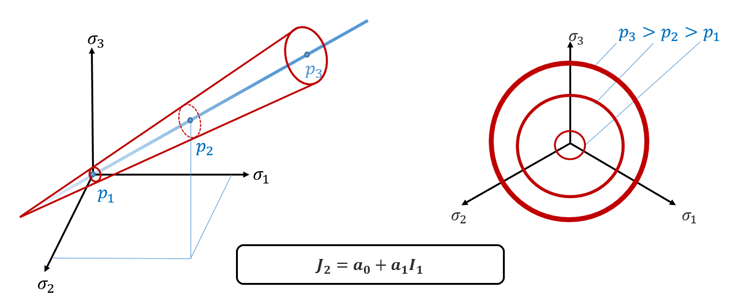
Figure 1. Original Drucker-Prager Yield Criteria

Radioss is using the extended Drucker-Prager yield criteria whose pressure dependency is nonlinear.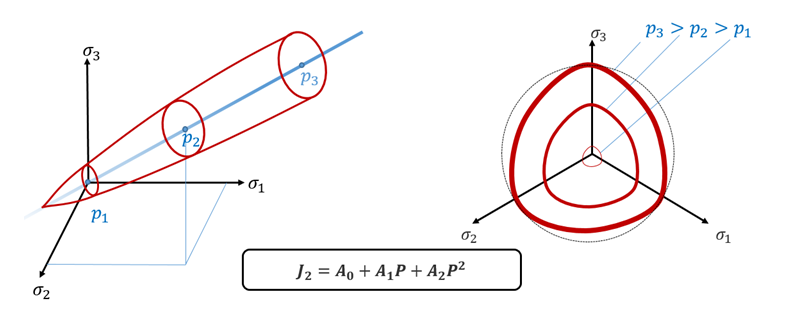

Figure 2. Extended Drucker-Prager Yield Criteria Implemented in Radioss
Extended Drucker-Prager yield criteria can be compared with Mohr-Coulomb criteria.

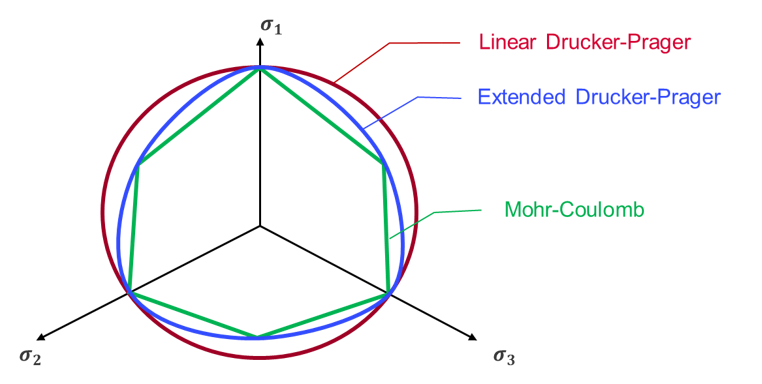
Figure 3. Extended Drucker-Prager Yield Criteria Implemented in Radioss versus Mohr-Coulomb Criteria

An extended Drucker-Prager yield criterion can be fitted from Mohr-Coulomb parameters:

$c$

Cohesion parameter

$ϕ$

Angle of internal friction

For this purpose, parameters $A_{0}, A_{1}, A_{2}$ must be defined as:(1)
$A_{0} = k {(c, ϕ)}^{2}$

$A_{1} = 6 k (c, ϕ) \times α (ϕ)$

$A_{2} = 9 α {(ϕ)}^{2}$

Modeling Type

Parameters

Circumscribed Drucker-Prager criteria

$\begin{array}{l} k = \frac{6 c \times \cos (ϕ)}{\sqrt{3} (3 - \sin (ϕ))} \\ α = \frac{2 \sin (ϕ)}{\sqrt{3} (3 - \sin (ϕ))} \end{array}$

Middle Circle

$\begin{array}{l} k = \frac{6 c \times \cos (ϕ)}{\sqrt{3} (3 + \sin (ϕ))} \\ α = \frac{2 \sin (ϕ)}{\sqrt{3} (3 + \sin (ϕ))} \end{array}$

Inscribed Drucker-Prager criteria

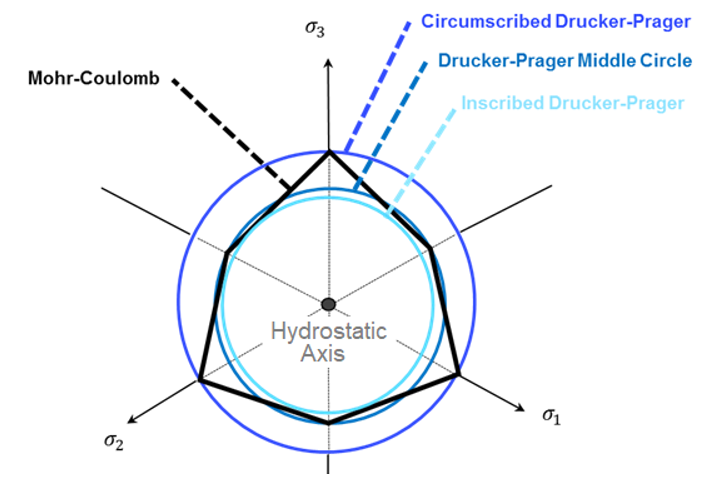
$\begin{array}{l} k = \frac{3 c \times \cos (ϕ)}{\sqrt{9 + 3 \sin^{2} (ϕ)}} \\ α = \frac{\sin (ϕ)}{\sqrt{9 + 3 \sin^{2} (ϕ)}} \end{array}$

Figure 4. Fitting a Drucker-Prager Yield Criteria (blue colors) from Mohr-Coulomb Criterion (black)
/MAT/LAW21 is also based on an extended Drucker-Prager yield criteria but pressure evolution can be described with user functions.
Young's modulus E and Poisson’s ratio $ν$ are used to determined shear modulus G which is required for sound speed calculation in solid materials.
Starter checks the yield parameters A₀, A₁, and A₂ and warns you in case of an unexpected situation.

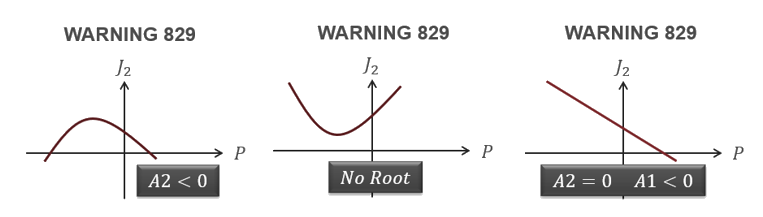Figure 5.