/MAT/LAW21 (DPRAG)

This law is similar to /MAT/LAW10 (DPRAG1); the only difference being that in this law, the pressure is input as a user-defined function of volumetric strain. This law is compatible only with solid elements.

Format

(1)	(3)	(5)	(7)
/MAT/LAW21/`mat_ID`/`unit_ID` or /MAT/DPRAG/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$ν$
`A`₀	`A`₁	`A`₂	`A`_max
`fct_ID`_f	`K`_t	`Fscale`_P
$Δ P_{\min}$	`P`_ext
`B`	$μ_{\max}$

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier (Integer, maximum 10 digits)
`mat_title`	Material title (Character, maximum 100 characters)
$ρ_{i}$	Initial density (Real)	$[\frac{kg}{m^{3}}]$
`E`	Young's modulus (Real)	$[Pa]$
$ν$	Poisson's ratio (Real)
`A`₀	Material plasticity coefficient. (Real)	$[P a^{2}]$
`A`₁	Material plasticity coefficient. (Real)	$[Pa]$
`A`₂	Material plasticity coefficient. (Real)
`A`_max	Limiting von Mises stress. Default set to 10³⁰ (Real)	$[P a^{2}]$
`fct_ID`_f	Function identifier describing $P (μ)$ . (Integer)
`K`_t	Tensile bulk modulus. 3 (Real)	$[Pa]$
`Fscale`_P	Pressure function scale factor. Default = 1.0 (Real)	$[Pa]$
$Δ P_{\min}$	Minimum pressure. Default = -10³⁰ (Real)	$[Pa]$
`P`_ext	External pressure. 4 Default = 0 (Real)
`B`	Unloading bulk modulus. 3 (Real)	$[Pa]$
$μ_{\max}$	Maximum volumetric strain in compression. 5 (Real)

Example (Sand)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/DPRAG/1/1
Sand
#        Init. dens.
              1.6E-9
#                  E                  Nu
                 100                  .3
#                 A0                  A1                  A2                Amax
                1E-7                .001                   1                   0
#       If                            Kt              Fscale
         2                             1                   0
#              P_min
             -1.5E-4
#                  B              Mu_max
                  80                  .4
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
Sand
#                  X                   Y
                  -1                   0                                                            
                   0                   0                                                            
                  .1                1000                                                            
                  .2                2500                                                            
                  .3                5000                                                            
                  .4               10000                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

Hydrodynamic behavior is given by a user-defined function $P = f (μ)$ .
Where,

P

Pressure in the material

$μ$

Volumetric strain with $μ = \frac{ρ}{ρ_{0}} - 1$

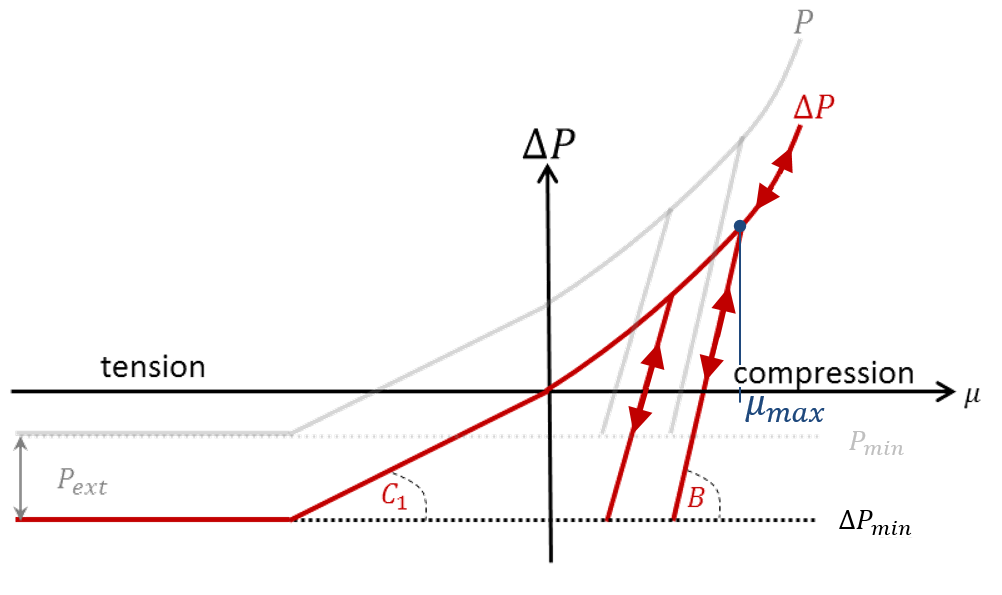
Figure 1.
Drucker-Prager yield criteria uses a modified von Mises yield criteria to incorporate the effects of pressure for massive structures:(1)
$F = J_{2} - (A_{0} + A_{1} P + A_{2} P^{2})$

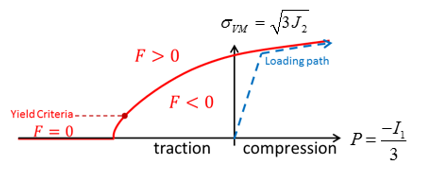
Figure 2.

Where,

$J_{2}$

Second invariant of deviatoric stress, with $σ_{V M} = \sqrt{3 J_{2}}$

P

Pressure, with $P = \frac{- I_{1}}{3}$ ( $I_{1}$ is the first stress invariant)

A₀, A₁, and A₂

Material plasticity coefficients

$A_{1} = A_{2} = 0$

Yield criteria is von Mises ( $σ_{V M} = \sqrt{3 A_{0}}$ )
It is recommended to set Unloading Bulk modulus, B is equal to the initial slope of function describing $P (μ)$ and Tensile Bulk modulus K_t equal to 1/100 of Unloading Bulk modulus B and K_t must be positive.
External pressure is needed in case of relative pressure formulation. In this specific case, yield criteria and energy integration require total pressure value. Radioss outputs a pressure which is relative to $P_{e x t}$ . You can conclude the total pressure value from:(2)
$P = P_{e x t} + Δ P$

Total pressure limit is concluded from:(3)
$P_{\min} = P_{e x t} + Δ P_{\min}$

If $P_{e x t} = 0$ , the output result is a total pressure:

$P = Δ P$ and $P_{\min} = Δ P_{\min}$
B is unloading bulk modulus. If B is defined, then it must be greater than any slope $\frac{d P}{d μ}$ in $[0, μ_{\max}]$ .
- If $B = 0$ and $μ_{\max} = 0$ , the unloading and loading paths are the same.
- If $B = 0$ or $μ_{\max} \neq 0$ , the default value for B is $B = {\frac{d P}{d μ} |}_{μ_{\max}}$ .
- If $B \neq 0$ or $μ_{\max} = 0$ , the default value for $μ_{\max}$ is $B = {\frac{d P}{d μ} |}_{μ_{\max}}$ .
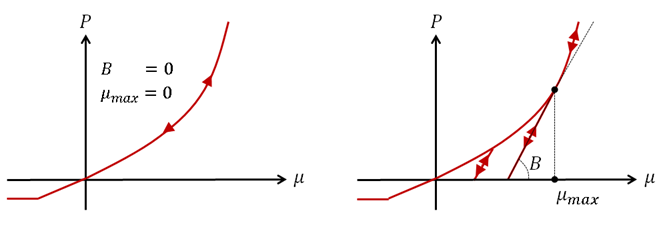
Figure 3.