Explanation of results
Reminder
The heat flux (or thermal flux) Φ is an algebraic quantity; from the physical point of view, this is power expressed in Watts.
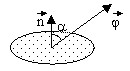
The heat flux traversing the surface S is the
integral ![]() , where the vector
quantity
, where the vector
quantity ![]() is the density of the
heat flux (or density of thermal flux).
is the density of the
heat flux (or density of thermal flux).
The lines tangent to vector ![]() are the
thermal flux lines.
are the
thermal flux lines.
Computation of the heat flux traversing a surface
For a surface perpendicular to the heat flux and a
homogeneous flux density on this surface, then ![]() .
.
For a surface where the normal ![]() in a
point is directed in an unspecified way with respect to the flux,
then the elementary heat flux is
in a
point is directed in an unspecified way with respect to the flux,
then the elementary heat flux is ![]() .
.
The flux traversing the surface S is computed by the integral ![]()
Thermal exchange balance
At steady state, the total power of heat sources delivered to a system must be equal to the sum of the heat flux exchanged with the ambient environment by the heat exchange surfaces.
Which results in:
![]()
where
-
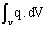 represents the represents the source power linked to
the given heat flux density
represents the represents the source power linked to
the given heat flux density -
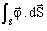 represents the heat flux exchanged with the ambient
environment by the heat exchange surfaces (also called losses
).
represents the heat flux exchanged with the ambient
environment by the heat exchange surfaces (also called losses
).
… in 2D
The Power and Losses commands enable the direct computation of the previously defined quantities.
… in 3D
It is necessary to use the Intégrale command in order to calculate the previous integrals.
- The power of the heat sources is obtained by the integration of the heat density source (dHeatL, dHeatS, dHeatV) on the conducting regions with sources.
- The heat flux exchanged with the ambient environment by a heat exchange surface is directly obtained by the integration of the surface density of heat exchange (dExchangeS ) .
- The heat flux exchanged with the external environment by the surfaces with imposed heat flux density or imposed temperature is obtainable as previously presented by the integration of the following formula (dFluxTh*N) on the appropriate surfaces.