Définition spatiale et temporelle
Introduction
Le calcul de forces est réalisé sur un support géométrique et éventuellement sur un intervalle de temps définis par l'utilisateur.
Pour des besoins de compatibilité avec le logiciel de mécanique, ou de réduction du temps de travail, des outils de reconstruction géométrique et de duplication temporelle sont disponibles.
Reconstruction géométrique 3D (automatique)
Le logiciel de mécanique est de dimension 3D. Par conséquent, quelque soit la géométrie Flux initiale, tous les fichiers exportés de Flux représentent des résultats en 3D.
Les reconstructions géométriques gérées par Flux lors de l'export sont les suivantes :
- Un projet 2D est reconstruit en 3D (avec le nombre d'éléments dans la profondeur spécifié par l'utilisateur lors de l'export)
- Pour un calcul sur le maillage de Flux, un projet partiel avec symétries et périodicités est reconstruit en projet complet (optionnel)
Duplication temporelle : présentation
Dans la boite de calcul de forces, il est possible à l'utilisateur de choisir l'application d'une duplication temporelle, pour les dispositifs ayant un comportement périodique dans le temps, notamment les moteurs. Cette duplication consiste à répercuter les valeurs calculées sur la plage de temps définie, pour obtenir automatiquement les valeurs sur une période mécanique.
Les avantages sont :
- Le calcul de forces est plus rapide
- Il n'y a pas besoin de résoudre le projet sur une période mécanique entière
Duplication temporelle : en pratique
L'utilisateur a la possibilité de choisir une plage de temps correspondant à une portion 1/n* de la période mécanique.
*n : un nombre entier, valant au minimum 2p (p : nombre de paires de pôles) pour les moteurs électriques
Duplication temporelle : mises en garde
- Mise en garde 1 : le point initial et final de la plage de temps doivent être
confondus. Par exemple, si la période est de 0.06 secondes on prendra :
- Une plage de 0.01 à 0.07 secondes sans duplication
- Une plage de 0.01 à 0.025 secondes avec une duplication de 4 fois
- Mise en garde 2 : Il ne faut pas prendre comme premier pas de calcul de forces le premier pas de calcul du scénario de résolution pour des raisons d'initialisations numérique
Duplication temporelle : vérification
La précision des résultats va dépendre de la plage de temps choisie. Si la fraction 1/n de la période n'est pas définie avec un n entier, alors les résultats seront faussés.
Dans la boite de calcul, une fois la plage de temps rentrée et le choix sur la duplication temporelle faits, l'utilisateur a le moyen de vérifier la précision de son calcul (avant de le lancer) en comparant :
- La fréquence mécanique réelle
- La fréquence mécanique calculée (avec la plage de temps choisie)
Le nombre de duplications (toujours un entier) est également donné, et un message indique la possibilité ou non pour le logiciel d'appliquer la duplication temporelle.
Exemple
L'image ci-dessous représente la partie sur l'intervalle temporel de calcul dans la boite de calcul. Dans ce cas-ci, la machine tourne à 1000 tours/min, la période mécanique est donc de 0.06 secondes. La machine a deux paires de pôles, donc on peut choisir une plage de temps au minimum égale à 1/2p=1/4 de la période (choix réalisé dans ce cas).
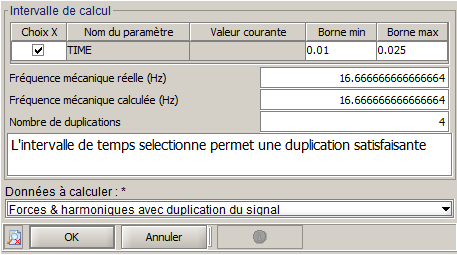
Pas de temps (analyse fréquentielle)
En application transitoire, l'utilisateur choisit lors de la création du scénario de résolution un intervalle de temps ainsi qu'un pas de temps de calcul. De plus, dans la boite de création d'un calcul de forces, un intervalle de temps représentant une période est choisi (ou une portion de la période si la duplication du signal a été choisi).
Dans le cas d'une analyse fréquentielle, le choix du pas de temps doit se faire en fonction du nombre d'harmoniques à analyser.
Le nombre d'harmoniques est déduit à partir du nombre de pas de temps dans la boite de calcul de forces comme expliqué dans le programme suivant :
N_step : nombre de pas de temps dans l'intervalle de la boite de calcul de forcesN_harm : nombre d'harmoniquesInitialisation: N_harm=2Tant que: (N_step-1)/2 >= N_harm :N_harm=N_harm*2N_harm est donc sous la forme : 2^n ; n étant un entier
Le N_harm obtenu représente le nombre d'harmoniques pour tout le spectre (fréquences positives et négatives).
Dans les applications physiques, uniquement la partie positive du spectre est considérée.
N_harm=N_harm/2Cette valeur est disponible dans la boite de calcul de forces éditée après un calcul, comme le montre l'image suivante :
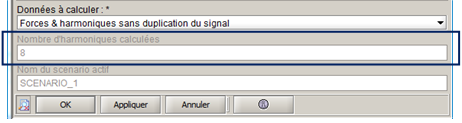
Le tableau suivant illustre le programme informatique précédent en donnant le nombre d'harmoniques calculées associé au nombre de pas :
Nombre de pas
Nombre d'harmoniques calculées
| Nombre de pas | Nombre d'harmoniques calculées |
|---|---|
| 6 à 8 | 2 |
| 9 à 16 | 4 |
| 17 à 32 | 8 |
| 33 à 64 | 16 |
| 65 à 128 | 32 |
| 129 à 256 | 64 |
| 257 à 512 | 128 |
| 513 à 1024 | 256 |
Le pas fréquentiel des harmoniques est défini par : f=1/T=1/(dt*(N_step-1));
Avec dt : le pas de temps et T : la période
La première harmonique a une fréquence de 0Hz (correspondant à la composante continue).