DIFFUSIVITY_MODEL
Specifies a diffusivity model for the species transport equations.
Type
AcuSolve Command
Syntax
CONDUCTIVITY_MODEL("name") {parameters...}
Qualifier
User-given name.
Parameters
- type (enumerated) [=none]
- Type of diffusivity.
- constant or const
- Constant diffusivity. Requires diffusivity.
- ramped or ramp
- Ramp the diffusivity to a constant value. Requires diffusivity.
- piecewise_linear or linear
- Piecewise linear curve fit. Requires curve_fit_values and curve_fit_variable.
- cubic_spline or spline
- Cubic spline curve fit. Requires curve_fit_values and curve_fit_variable.
- user_function or user
- User-defined function. Requires user_function, user_values and user_strings.
- diffusivity or diff (real) >=0 [=0]
- Constant value of diffusivity. Used with constant and ramped types.
- curve_fit_values or curve_values (array) [={0,0}]
- A two-column array of independent-variable/diffusivity data values. Used with piecewise_linear and cubic_spline types.
- curve_fit_variable or curve_var (enumerated) [=temperature]
- Independent variable of the curve fit. Used with piecewise_linear and
cubic_spline types.
- x_coordinate or xcrd
- X-component of coordinates.
- y_coordinate or ycrd
- Y-component of coordinates.
- z_coordinate or zcrd
- Z-component of coordinates.
- x_reference_coordinate or xrefcrd
- X-component of reference coordinates.
- y_reference_coordinate or yrefcrd
- Y-component of reference coordinates.
- z_reference_coordinate or zrefcrd
- Z-component of reference coordinates.
- temperature or temp
- Temperature.
- species_1 or spec1
- Species 1.
- species_2 or spec2
- Species 2.
- species_3 or spec3
- Species 3.
- species_4 or spec4
- Species 4.
- species_5 or spec5
- Species 5.
- species_6 or spec6
- Species 6.
- species_7 or spec7
- Species 7.
- species_8 or spec8
- Species 8.
- species_9 or spec9
- Species 9.
- user_function or user (string) [no default]
- Name of the user-defined function. Used with user_function type.
- user_values (array) [={}]
- Array of values to be passed to the user-defined function. Used with user_function type.
- user_strings (list) [={}]
- Array of strings to be passed to the user-defined function. Used with user_function type.
- multiplier_function (string) [=none]
- User-given name of the multiplier function for scaling the viscosity. If none, no scaling is performed.
- turbulent_schmidt_number or turb_sc (real) >0 [=0.91]
- Value of the turbulent Schmidt number. Used with turbulence models.
Description
This command specifies a diffusivity model for the species transport equations. This model is only applicable to fluid element sets.
DIFFUSIVITY_MODEL( "my diffusivity model" ) {
type = constant
diffusivity = 1
}
MATERIAL_MODEL( "my material model" ) {
diffusivity_1_model = "my diffusivity model"
...
}
ELEMENT_SET( "fluid elements" ) {
material_model = "my material model"
...
}where d is the diffusivity for species
A constant diffusivity model applies a spatially constant diffusivity, as in the above example.
DIFFUSIVITY_MODEL( "ramped diffusivity model" ) {
type = ramped
diffusivity = 1
}starts at diffusivity of 1000 at time step one and reduces the diffusivity until time step 10, at which time a diffusivity of one is used.
DIFFUSIVITY_MODEL( "curve fit diffusivity model" ) {
type = piecewise_linear
curve_fit_values = { 273, 1.0 ;
323, 1.1 ;
373, 1.3 ;
423, 1.6 ;
curve_fit_variable = temperature
}defines diffusivity as a function of temperature. In this case, the problem must contain a temperature equation; see the EQUATION command. The curve_fit_values parameter is a two-column array corresponding to the independent variable and the diffusivity values. The independent variable values must be in ascending order. The limit point values of the curve fit are used when curve_fit_variable falls outside of the curve fit limits.
273 1.0
323 1.1
373 1.3
423 1.6DIFFUSIVITY_MODEL( "curve fit diffusivity model" ) {
type = piecewise_linear
curve_fit_values = Read( "diffusivity.fit"
curve_fit_variable = temperature
}A diffusivity of type user_function may be used to model more complex behaviors; see the AcuSolve User- Defined Functions Manual for a detailed description of user-defined functions.
DIFFUSIVITY_MODEL( "UDF diffusivity model" ) {
type = user_function
user_function = "usrDiffusivityExample"
user_values = { 1.0, # constant value
0.1, # temperature scale
0.2 } # species scale
}#include "acusim.h"
#include "udf.h"
UDF_PROTOTYPE( usrDiffusivityExample ) ; /* function prototype */
Void usrDiffusivityExample (
UdfHd udfHd, /* Opaque handle for accessing data */
Real* outVec, /* Output vector */
Integer nItems, /* Number of elements */
Integer vecDim /* = 1 */
) {
Integer elem ; /* an element counter */
Real diff0 ; /* reference diffusivity */
Real sScale ; /* species scale */
Real tScale ; /* temperature scale */
Real* spec ; /* species field */
Real* temp ; /* temperature field */
Real* usrVals ; /* user values */
udfCheckNumUsrVals( udfHd, 3 ) ; /* check for error */
usrVals = udfGetUsrVals( udfHd ) ; /* get the user vals */
diff0 = usrVals[0] ; /* reference diff. */
tScale = usrVals[1] ; /* temp. scale */
sScale = usrVals[2] ; /* spec. scale */
temp = udfGetElmData( udfHd, UDF_ELM_TEMPERATURE ) ; /* get temperature */
spec = udfGetElmData( udfHd, UDF_ELM_SPECIES ) ; /* get species */
for ( elem = 0 ; elem < nItems ; elem++ ) {
outVec[elem] = diff0
+ tScale * temp[elem]
+ sScale * spec[elem] ;
}
} /* end of usrDiffusivityExample() */The dimension of the returned diffusivity vector, outVec, is the number of elements.
DIFFUSIVITY_MODEL( "similar to ramped diffusivity model" ) {
type = constant
diffusivity = 1
multiplier_function = "ramped"
}
MULTIPLIER_FUNCTION( "ramped" ) {
type = piecewise_log_linear
curve_fit_values = { 1, 1000 ; 10, 1 }
curve_fit_variable = time_step
}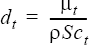
where t is the turbulent viscosity, given by the turbulence model in use; is the density; and SCt is the turbulent Schmidt number, given by turbulent_schmidt_number.