FINITE_MASS

Specifies the finite mass model parameters.

Type

AcuTrace Command

Syntax

FINITE_MASS {parameters}

Qualifier

This command has no qualifier.

Parameters

drag_law_type or drag_law (enumerated)[=standard]

Type of drag law.

zero or none: No drag force.
simple_stokes_law or simple: Simple Stokes law.
stokes_law or stokes: Stokes law.
standard_drag_law or standard: Standard drag law.

drag_coefficient_model or cd_model (enumerated)[=standard]

Type of drag coefficient model. Used only when drag_law_type is standard.

constant: Constant drag coefficient.
standard: Standard drag coefficient model.

drag_coefficient or cd (real) [=0.0]

Drag coefficient. Used only when drag_law_type is standard and drag_coefficient_model is constant or when drag_law_type is simple.

faxen_drag_force or faxen_drag (boolean) [=on]

Flag specifying if Faxen force is used. Used only when drag_law_type is standard or stokes.

viscosity_model or mu_model (enumerated) [=flow]

Flag specifying how to obtain the values of material viscosity used to compute the Reynolds number. Used only when drag_law_type is standard.

use_flow_values or flow: Obtain the values from the AcuSolve database.
constant: Use a constant value.

constant_viscosity or mu (real) [=0.0]

Material viscosity used in calculations of the Reynolds number. Used only when drag_law_type is standard and viscosity_model is constant.

density_model or rho_model (enumerated)[=flow]

Flag specifying how to obtain the values of fluid density used in force calculations.

use_flow_values or flow: Obtain the values from the AcuSolve database.
constant: Use a constant value.

constant_density or rho_fluid (real) [=0.0]

Fluid density used in force calculations. Used only when density_model is constant.

pressure_force or pressure (boolean) [=on]

Flag specifying if pressure force is used.

tau_force or tau (boolean) [=on]

Flag specifying if viscous stress force is used.

virtual_mass_force or virtual_mass (boolean) [=on]

Flag specifying if virtual mass force is used.

faxen_virtual_mass_force or faxen_virtual_mass (boolean) [=on]

Flag specifying if Faxen virtual mass force is used. Used only when faxen_drag is on.

constant_gravity or gravity (array) [={0,0,0}]

Acceleration due to gravity. This value should equal what is used in AcuSolve.

centrifugal (boolean) [=on]

Flag specifying if the centrifugal acceleration is included in rotating reference frames. This value should equal what is used in AcuSolve.

coriolis (boolean) [=on]

Flag specifying if the coriolis acceleration is included in rotating reference frames. This value should equal what is used in AcuSolve.

angular_acceleration or angular_acc (boolean) [=on]

Flag specifying if the angular acceleration is included in rotating reference frames. This value should equal what is used in AcuSolve.

wall_type or type (enumerated) [=reflect]

Wall type. Applies only to particle surfaces of type wall, slip, or symmetry not specified in a FINITE_MASS_BOUNDARY_CONDITION command.

reflect: Particles reflect at surface.
stop or trap: Particles stop at surface but remain active.
terminate or escape: Particles stop at surface and become inactive.

wall_en_type or en_type (enumerated) [=constant]

Type of normal coefficient of restitution. Applies only to particle surfaces of type wall, slip, or symmetry not specified in a FINITE_MASS_BOUNDARY_CONDITION command and only if wall_type is reflect.

constant: Coefficient is constant.
piecewise_linear or linear: Coefficient is a piecewise linear function of the normal component of the impact velocity.
cubic_spline or spline: Coefficient is a cubic spline function of the normal component of the impact velocity.

constant_wall_en or wall_en [=1.0]

Normal coefficient of restitution. Applies only to particle surfaces of type wall, slip, or symmetry not specified in a FINITE_MASS_BOUNDARY_CONDITION command and only if wall_type is reflect and wall_en_type is constant.

wall_en_curve_fit_values or en_values [no default]

A two-column array of normal-velocity/normal-coefficient-of-restitution data values. Used when wall_en_type is piecewise_linear or cubic_spline. Applies only to particle surfaces of type wall, slip, or symmetry not specified in a FINITE_MASS_BOUNDARY_CONDITION command and only if wall_type is reflect.

wall_et_type or et_type (enumerated) [=constant]

Type of tangential coefficient of restitution. Applies only to particle surfaces of type wall, slip, or symmetry not specified in a FINITE_MASS_BOUNDARY_CONDITION command and only if wall_type is reflect.

constant: Coefficient is constant.
piecewise_linear or linear: Coefficient is a piecewise linear function of the normal component of the impact velocity.
cubic_spline or spline: Coefficient is a cubic spline function of the normal component of the impact velocity.

constant_wall_et or wall_et [=1.0]

Tangential coefficient of restitution. Applies only to particle surfaces of type wall, slip, or symmetry not specified in a FINITE_MASS_BOUNDARY_CONDITION command and only if wall_type is reflect and wall_en_type is constant.

wall_et_curve_fit_values or et_values [no default]

A two-column array of normal-velocity/tangential-coefficient-of-restitution data values. Used when wall_et_type is piecewise_linear or cubic_spline. Applies only to particle surfaces of type wall, slip, or symmetry not specified in a FINITE_MASS_BOUNDARY_CONDITION command and only if wall_type is reflect.

Description

The FINITE_MASS command specifies the forces acting on the particles and the default particle/wall interaction.

The forces acting on a particle in AcuTrace are

(1)

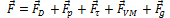
where ${\vec{F}}_{D}$ is the drag force, ${\vec{F}}_{p}$ the pressure force, ${\vec{F}}_{τ}$ the viscous stress force, ${\vec{F}}_{V M}$ the virtual mass force, and ${\vec{F}}_{g}$ the gravity force. (The Basset force and other forces such as the Saffman lift force are not currently accounted for.) The parameters drag_law_type, pressure_force, tau_force, virtual_mass_force, and constant_gravity determine which of these are active; by default, all forces are active. Note that the default value of constant_gravity is the zero vector; this should be set to the same value used in the AcuSolve run providing the flow data for the trace.

The drag and the virtual mass forces can include Faxen correction terms accounting for nonuniformity effects. The inclusion of these terms is controlled by the parameters faxen_drag_force and faxen_virtual_mass. These terms are included by default. Generally, none of the force-related parameters need to be modified with the exception of constant_gravity.

By default (drag_law_type is standard and drag_coefficient_model is standard) the drag force (without the Faxen correction) is ${\vec{F}}_{D} = - C_{D} \frac{π}{g} ρ_{f} d_{p}^{2} | {\vec{u}}_{p} - {\vec{u}}_{f} | ({\vec{u}}_{p} - {\vec{u}}_{f})$ where $ρ_{f}$ is the density of the fluid and $d_{p}^{}$ the diameter of the particle. The value of $C_{D}$ the coefficient of drag, depends on the relative Reynolds number, $Re = \frac{ρ_{f} d_{p} | {\vec{u}}_{p} - {\vec{u}}_{f} |}{μ}$ where $μ$ is the material viscosity of the fluid:

(2)

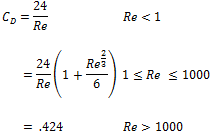
When drag_law_type is standard and drag_coefficient_model is constant, $C_{D}$ is equal to the value of drag_coefficient regardless of the value of Re. When drag_law_type is stokes_law, ${\vec{F}}_{D} = - 3 π μ d_{p} ({\vec{u}}_{p} - {\vec{u}}_{f})$ (i.e. $C_{D} = \frac{24}{Re}$ ) regardless of the value of Re. When drag_law_type is simple_stokes, ${\vec{F}}_{D} = - C_{D} ({\vec{u}}_{p} - {\vec{u}}_{f})$ where $C_{D}$ is equal to the value of drag_coefficient. When drag_law_type is zero, ${\vec{F}}_{D}$ is the zero vector.

The other forces are

(3)

\begin{array}{l} {\vec{F}}_{p} = V_{p} \nabla p \\ {\vec{F}}_{τ} = V_{p} \nabla \cdot τ \\ {\vec{F}}_{V M} = ρ_{f} \frac{V_{p}}{2} (\frac{D {\vec{u}}_{f}}{D t} - \frac{D {\overset{⇀}{u}}_{p}}{D t}) \\ {\vec{F}}_{g} = m_{p} \vec{g} \end{array}

where $V_{p}$ is the volume of the particle $ρ$ the fluid pressure, $τ$ the viscous stress tensor of the fluid, and $\frac{D {\vec{u}}_{f}}{D t}$ the material derivative of the fluid velocity. $\vec{g}$ is given by the value of constant_gravity. If pressure_force, tau_force, or virtual_mass_force are off, ${\vec{F}}_{p}$ , ${\vec{F}}_{τ}$ , or ${\vec{F}}_{V M}$ respectively, are set to 0. Similarly, if faxen_drag_force or faxen_virtual_mass_force are off, the corresponding Faxen correction is set to 0.

Note that the calculation of the drag and the virtual mass forces requires values for the fluid density and, in the case of drag, material viscosity. It is highly recommended that these values be obtained from the AcuSolve database, for example,

density_model       = use_flow_values
viscosity_model     = use_flow_values

However, these values are in the AcuSolve database only if derived quantity output is enabled in AcuSolve. This output is enabled only if the output_frequency parameter in the DERIVED_QUANTITY_OUTPUT command has a non-zero value, for example,

DERIVED_QUANTITY_OUTPUT {
...
   output_frequency    = 1000
...
}

Moreover, if density_model = use_flow_values or viscosity_model = use_flow_values, AcuTrace requires that the output_frequency parameters in the AcuSolve NODAL_OUTPUT and DERIVED_QUANTITY_OUTPUT commands have the same value, for example,

DERIVED_NODAL_OUTPUT {
...
   output_frequency    = 1000
...
}
DERIVED_QUANTITY_OUTPUT {
...
   output_frequency    = 1000
...
}

If AcuTrace is run with density_model or viscosity_model equal to use_flow_values and derived quantity output was not enabled in the AcuSolve run, AcuTrace will print an error message and stop. AcuTrace will also stop if density_model or viscosity_model equals use_flow_values and there is a mismatch in the values of output_frequency in AcuSolve. In either of these cases, the two options are either to rerun AcuSolve with the proper inputs or to use

density_model       = constant
viscosity_model     = constant

and suitable values of constant_density and constant_viscosity.

The default particle-wall boundary conditions and interaction parameters are also set by the FINITE_MASS command. Only the interactions at surfaces of type wall, slip, or symmetry are affected by the FINITE_MASS command. Moreover, the settings for a specific surface can be set in a FINITE_MASS_BOUNDARY_CONDITION command, in which case all the settings in the FINITE_MASS command, including default vales, are ignored for that surface.

AcuTrace allows three different types of interaction when a particle hits a wall (here "wall" refers to a surface of type wall, slip, or symmetry):

the particle reflects off the wall (wall_type = reflect)
the particle stops but continues to be actively involved in the particle trace (wall_type = stop)
the particle trace terminates (wall_type = terminate)

When a particle reflects off a wall, the normal and tangential components of its velocity ${\vec{u}}_{n}$ and ${\vec{u}}_{t}$ (in the wall frame of reference) are given by

(4)

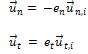
where $e_{n}$ and $e_{t}$ are the normal and tangential coefficients of restitution, and ${\vec{u}}_{n, i}$ and ${\vec{u}}_{t, i}$ are the incident values of the normal and tangential components of the particle velocity. $e_{n}$ and $e_{t}$ always lie between 0 and 1.

Each coefficient can be specified as a constant, a piecewise linear function of the magnitude of the incident normal velocity, or a cubic spline function of the magnitude of the incident normal velocity. Note that AcuTrace clips the values of the coefficients so that they lie between 0 and 1.

In the first example below, the normal and tangential coefficients of restitution have constant values of 1.0:

wall_en_type        = constant 
wall_et_type        = constant 
wall_en             = 1.0
wall_et             = 1.0

In the next example, the normal and tangential coefficients of restitution have values of .1, .5, and .9 for incident normal velocity magnitudes of 1, 10, and 100, respectively. Linear interpolation is used for velocity magnitudes between 1 and 100; constant extrapolation is used for magnitudes less than 1 or greater than 100:

wall_en_type        = piecewise_linear
wall_et_type        = piecewise_linear
en_values           = { 1.0, 0.1 ;
                          10.0, 0.5 ;
                          100.0, 1.0 }
et_values           = { 1.0, 0.1 ;
                          10.0, 0.5 ;
                          100.0, 1.0 }

If instead

wall_en_type        = cubic_spline
wall_et_type         = cubic_spline

cubic spline interpolants are used for velocity magnitudes between 1 and 100.