Turbulent Mixing Layers in an Open Channel

In this application, AcuSolve is used to simulate the mixing of two streams of fluid with different velocities moving past a splitter plate. AcuSolve results are compared with experimental results as described in J. Delville, et al. (1989). The close agreement of AcuSolve results with the experimental results validates the ability of AcuSolve to model mixing layers in the turbulent flow regime.

Problem Description

The problem consists of two streams of fluid having material properties of standard air with density of 1.2 kg /m3 and molecular viscosity of 1.7189 kg/m-sec. The two fluid streams enter an open channel separated by a splitter plate at two streamwise locations with differing velocities. The length of the channel is 1.8 m for the top portion and 1.5 m for the bottom portion. The inlet velocity of the top section is 41.54 m/s, producing a Reynolds's number of 2900, based on l=1.0 mm, while the inlet velocity of the lower section is 22.4 m/s, giving a Reynolds's number of 1200, as shown in the following image, which is not drawn to scale. The model is simulated as steady state with constant inflow conditions, using the Spalart Allmaras (SA) turbulence model. The velocity profile is computed for several locations downstream of the splitter plate and compared against the experimental data, as described in Delville, 1989.


Figure 1. Critical Dimensions and Parameters Used for Simulating the Turbulent Mixing Layer


Figure 2. Mesh used for Simulating the Turbulent Mixing Layer Showing Close up Images Near the Trailing Edge of the Plate

The simulation was performed as a two dimensional problem by constructing a volume mesh that contains a single layer of elements extruded in the cross stream direction, normal to the flow plane and by imposing symmetry boundary conditions on the extruded planes. The upper and lower walls are specified as slip, the splitter plate is specified as no-slip and the inlet velocity and eddy viscosity are prescribed as constant values.

AcuSolve Results

The AcuSolve solution converged to a steady state and the results reflect the mean flow conditions within the open channel. The simulation result shows a developing flow field with the fluids fully separated as they pass the edge of the splitter plate. As the fluid travels downstream of the splitter plate, the dissimilar velocity fields produce a shear layer that results in momentum exchange between the two streams. The shear layer diffuses as the fluid travels further downstream. The relative velocity as a function of the normalized boundary layer height is computed from AcuSolve and compared with experimental data at three measurement stations, 0.2 m, 0.65 m and 0.95 m away from the trailing edge of the plate, as described in Delville, 1989. The image below shows black circles representing the experimental data and a solid red line for the AcuSolve results.


Figure 3. Relative Velocity within the Channel Compared Against Experimental Data Showing Experimental and Simulated Results for the SA Turbulence Model


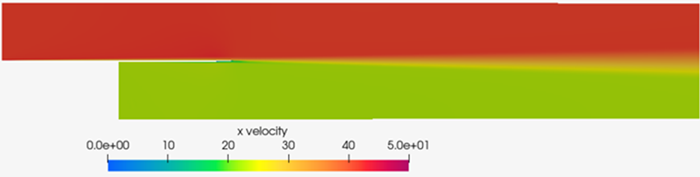
Figure 4. Velocity Magnitude Within the Channel

Summary

The AcuSolve solution compares well with experimental data for turbulent mixing within an open channel. In this application, the shear layer resulting from the dissimilar velocities of the incoming fluid streams results in an exchange of momentum within the channel. The amount of numerical dissipation from the grid is kept to a minimum to produce a good agreement with the experimental data. The good agreement with experimental results for the simulated turbulence model compares well with the measurement and previously published results, demonstrating that AcuSolve is capable of predicting turbulent mixing layers with relatively modest grid levels and the one equation turbulence model.

Simulation Settings for Turbulent Mixing Layers in an Open Channel

HyperWorks CFD database file: <your working directory>\mixing_layer_turbulent\mixing_layer_turbulent.hm

Global

  • Problem Description
    • Analysis type - Steady State
    • Turbulence equation - Spalart Allmaras
  • Auto Solution Strategy
    • Max time steps - 100
    • Convergence tolerance - 0.001
    • Relaxation Factor- 0.4
  • Material Model
    • Air
      • Type - Constant
      • Density - 1.2 kg/m3
      • Viscosity - 1.7189e-5 kg/m*sec

    Model

  • Volumes
    • Volume
      • Element Set
        • Material model - Air
  • Surfaces
    • Back
      • Simple Boundary Condition
        • Type- Symmetry
    • Front
      • Simple Boundary Condition
        • Type- Symmetry
    • InletLower
      • Simple Boundary Condition
        • Type- Inflow
        • Inflow type- Velocity
        • X Velocity- 22.4 m/sec
        • Turbulence input type- Direct
        • Eddy Viscosity- 0.0001432
    • InletUpper
      • Simple Boundary Condition
        • Type- Inflow
        • Inflow type- Velocity
        • X Velocity- 41.54 m/sec
        • Turbulence input type- Direct
        • Eddy Viscosity- 0.0001432
    • Outlet
      • Simple Boundary Condition
        • Type - Outflow
    • Slip
      • Simple Boundary Condition
        • Type- Slip
    • SplitterPlate
      • Simple Boundary Condition
        • Type - Wall
    • TE
      • Simple Boundary Condition
        • Type- Wall

References

Delville, J., Bellin, S., Garem, J. H., and Bonnet J. P., "Analysis of Structures in a Turbulent, Plane Mixing Layer by Use of a Pseudo Flow Visualization Method Based on Hot-Wire Anemometry," in: Advances in Turbulence 2, eds: H.-H. Fernholz and H. E. Fiedler, Proceedings of the Second European Turbulence Conference, Berlin, Aug. 30-Sept. 2, 1988, Springer Verlag, Berlin, 1989, pp. 251-256.