ACU-T: 5201 Coupled Simulation of a Check Valve using AcuSolve and MotionSolve

Prerequisites

This tutorial introduces you to the workflow for setting up an AcuSolve-MotionSolve co-simulation using HyperWorks CFD. Prior to starting this tutorial, you should have already run through the introductory HyperWorks tutorial, ACU-T: 1000 HyperWorks UI Introduction, and have a basic understanding of HyperWorks CFD and AcuSolve. To run this simulation, you will need access to a licensed version of HyperWorks CFD, MotionSolve, and AcuSolve.

Prior to running through this tutorial, click here to download the tutorial models. Extract ACU-T5201_pressureCheckValve.x_t and Valve_model.xml from HyperWorksCFD_tutorial_inputs.zip.

Problem Description

The problem to be addressed in this tutorial is shown schematically in Figure 1. It consists of a cylindrical pipe containing water that flows past a check valve with a shutter attached to a virtual spring (not included in the geometry). The inlet pressure varies over time and the movement of the shutter will be determined as a function of the balance of the fluid forces against the reactive force of the spring. The problem is rotationally periodic at 30° increments about the longitudinal axis, and it is assumed that the resulting flow is also rotationally periodic, allowing for modeling with the use of a wedge-shaped section. For this tutorial, a 30° section of the geometry is modeled, as shown in the figure. Modeling a portion of an rotationally periodic geometry leads to reduced computation time while still providing an accurate solution.


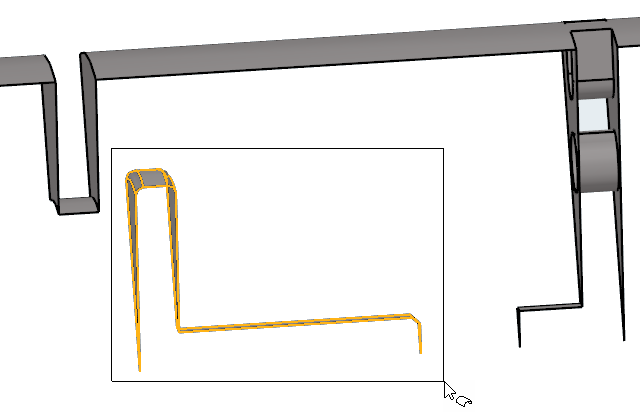
Figure 1. Schematic of Check Valve with Spring-Loaded Shutter

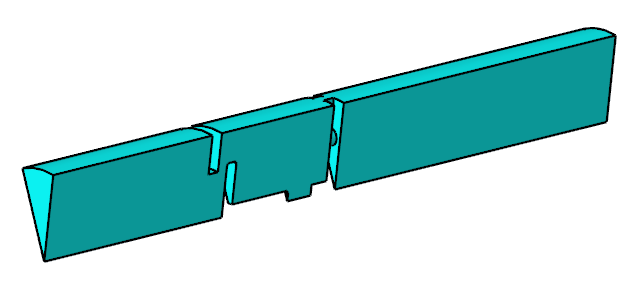
The pipe has an inlet diameter of 0.08 m and is 0.3 m long. The check-valve assembly is 0.085 m downstream of the inlet. It consists of a plate 0.005 m thick with a centered orifice 0.044 m in diameter and a shutter with an initial position 0.005 m from the opening, simulating a nearly closed condition. The shutter plate is 0.05 m in diameter and 0.005 m thick. The shutter plate is attached to a stem 0.03 m long and 0.01 m in diameter. The mass of the shutter and stem is 0.2 kg and its motion is affected by a virtual spring with a stiffness of 2162 N/m. The motion of the valve shutter is limited by a stop mounted on a perforated plate downstream of the shutter.

Note that AcuSolve's internal rigid-body-dynamics solver is not able to simulate contact. Therefore, this problem is formulated to avoid contact between the valve and the stop.

Modeling the geometry as a 30° section requires that the fluid model is set up to be consistent with the rigid-body model. Since only 1/12 of the rigid body is modeled, the forces computed by AcuSolve that act on the valve shutter represent 1/12 of the actual force on the device. Therefore, it is also necessary to account for this in the simulation. There are two methods that can be used to accomplish this:
  1. Scale up the fluid forces calculated by AcuSolve by a factor of 12 to represent the full load on the device when the displacement of the body is computed.

    Using this approach, the full stiffness of the valve spring is used in the rigid-body solution, and the full mass of the valve is used.

  2. Scale down the mass of the valve and the stiffness of the spring to by a factor of 12 to match the fraction of the valve geometry to be modeled.

    Using this approach, the loading passed to the rigid-body solver is not scaled.

This second approach is used in this tutorial; the scaled mass of 0.0167 kg and the scaled stiffness of 180.1667 N/m will be used

The fluid in this problem is water, which has a density (ρ) of 1000 kg/m3 and a molecular viscosity (μ) of 1 X 10-3 kg/m-sec.

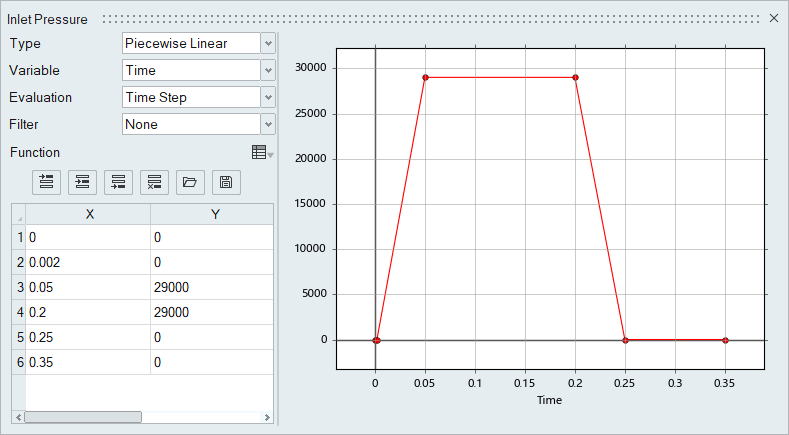
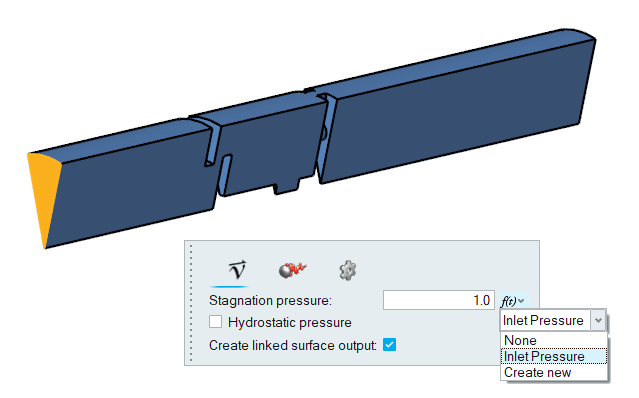
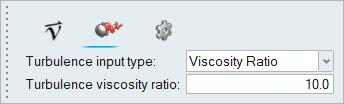
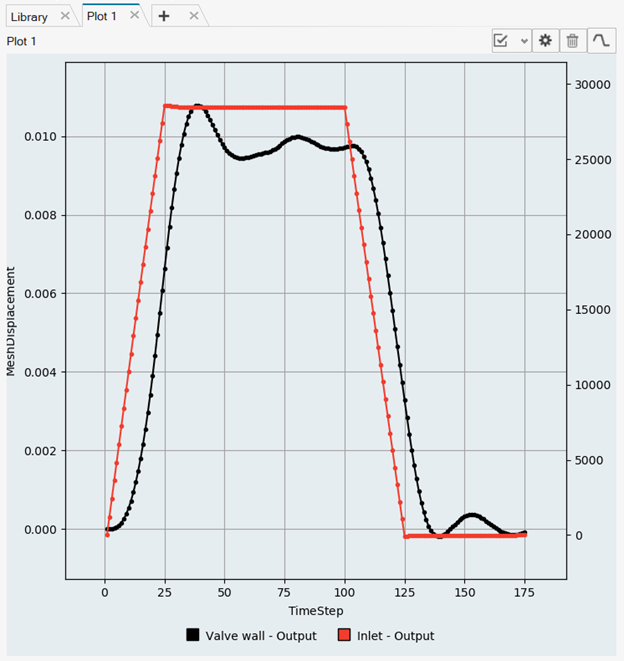
At the start of the simulation, the flow field is stationary. Flow is driven by the pressure at the inlet, which varies over time as a piecewise linear function shown in Figure 2. As the pressure at the inlet rises, the flow will accelerate as the valve opens. The turbulence viscosity ratio is assumed to be 10.

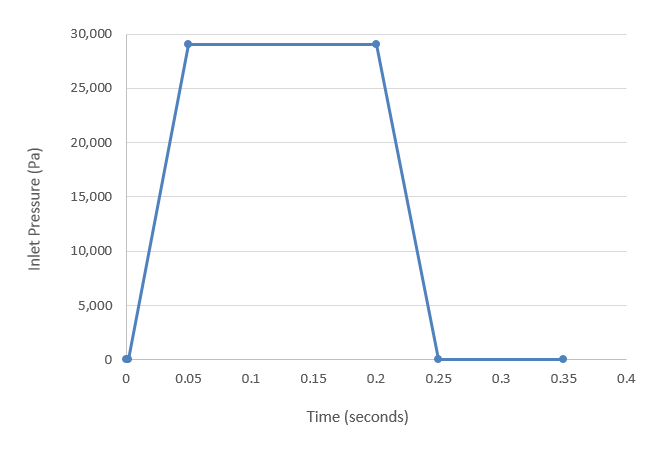
The initial inlet pressure is 0 Pa. At 0.002 s the pressure begins to ramp up and reaches 29,000 Pa at 0.05 s. The pressure is held at 29,000 Pa and begins to ramp back down starting at 0.2 s, reaching the initial pressure at 0.25 s where it remains for the rest of the simulation.


Figure 2. Transient pressure at the inlet

Prior simulations of this geometry indicate that the average velocity at the inlet reaches a maximum of 0.98 m/s. At this velocity, the Reynolds number for the flow is 78,400. When the Reynolds number is above 4,000 it is generally accepted that flow should be modeled as turbulent.

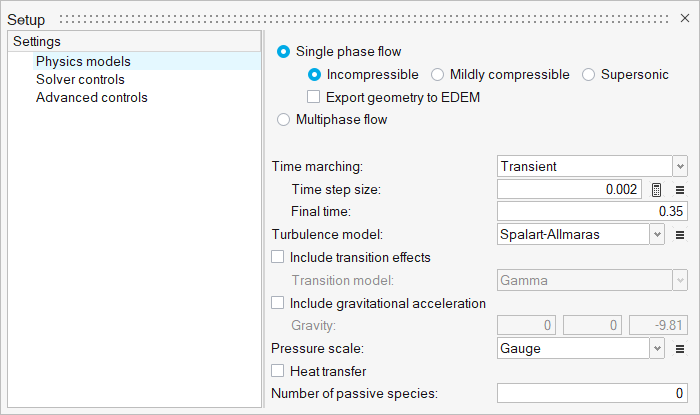
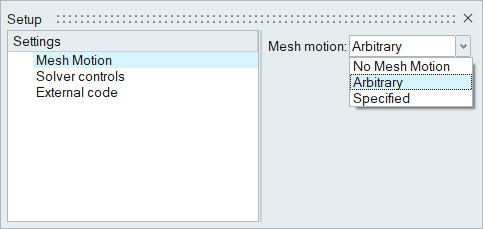
Note that the initial conditions of the flow are actually laminar; however, the increase in flow velocity and flow around the valve shutter is expected to cause a rapid transition to turbulent conditions. Therefore, the simulation will be set up to model transient, turbulent flow. When performing a transient analysis, convergence is achieved at every time step based on the defined stagger criteria. Mesh motion will be modeled using arbitrary mesh movement (arbitrary Lagrangian-Eulerian mesh motion).

For this case, the transient behavior of interest occurs in the time it takes for the pressure to ramp up and ramp back down, which is given by the transient pressure profile. To allow time for the spring to recover additional time will be simulated. For this tutorial 0.1 s is added after the pressure drops back to initial conditions for a total duration of 0.35 s.

Another critical decision in a transient simulation is choosing the time increment. The time increment is the change in time during a given time step of the simulation. It is important to choose a time increment that is short enough to capture the changes in flow properties of interest, but does not require unnecessary computation time. The change in inlet pressure from initial conditions to maximum occurs over 0.048 s. A time increment of 0.002 s would allow for excellent resolution of the transient changes without requiring excessive computational time.

Start HyperWorks CFD and Create the HyperMesh Model Database

  1. Start HyperWorks CFD from the Windows Start menu by clicking Start > Altair <version> > HyperWorks CFD.
    When HyperWorks CFD is loaded, the Geometry ribbon is open by default.
  2. Create a new .hm database in one of the following ways:
    • From the menu bar, click File > Save.
    • From the Home tools, Files tool group, click the Save As tool.


      Figure 3.
  3. In the Save File As dialog, navigate to the directory where you would like to save the database.
  4. Enter CheckValve_Coupled as the name for the database then click Save.
    This will be your problem directory and all the files related to the simulation will be stored in this location.
  5. Move the Valve_model.xml file to the problem directory.

Import and Validate the Geometry

Import the Geometry

  1. From the menu bar, click File > Import > Geometry Model.
  2. In the Import File dialog, browse to your working directory then select ACU-T5201_pressureCheckValve.x_t and click Open.
  3. In the Geometry Import Options dialog, leave all the default options unchanged then click Import.


    Figure 4.


    Figure 5.

Validate the Geometry

  1. From the Geometry ribbon, click the Validate tool.


    Figure 6.
    The Validate tool scans through the entire model, performs checks on the surfaces and solids, and flags any defects in the geometry, such as free edges, closed shells, intersections, duplicates, and slivers.

    The current model doesn’t have any of the issues mentioned above. Alternatively, if any issues are found, they are indicated by the number in the brackets adjacent to the tool name.

    Observe that a blue check mark appears on the top-left corner of the Validate icon. This indicates that the tool found no issues with the geometry model.


    Figure 7.
  2. Press Esc or right-click in the modeling window and swipe the cursor over the green check mark from right to left.
  3. Save the database.

Set Up Flow

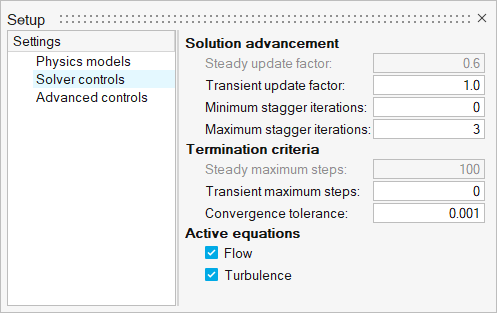
Set Up the Simulation Parameters and Solver Settings

  1. From the Flow ribbon, click the Physics tool.


    Figure 8.
    The Setup dialog opens.
  2. Under the Physics models setting:
    1. Set Time marching to Transient.
    2. Set the Time step size to 0.002 and the Final time to 0.35.
    3. Select Spalart-Allmaras as the Turbulence model.


    Figure 9.
  3. Click the Solver controls setting and set the Maximum stagger iterations to 3.
    Figure 10.
  4. Close the dialog and save the model.

Create a Multiplier Function for the Inlet Pressure

  1. From the Flow ribbon, click the arrow next to the Setup tool set, then select Multipliers.


    Figure 11.
  2. Click in the Multiplier Library dialog.
  3. In the multiplier creation dialog, change the name of the multiplier function to Inlet Pressure by clicking on the top-left corner.
  4. Set the Type to Piecewise Linear.
  5. Verify that the Variable is set to Time and Evaluation is set to Time Step.
  6. Click four times to add four rows to the bottom of the table.
  7. Enter the table values according to the image below.


    Figure 12.

Assign Material Properties

  1. From the Flow ribbon, click the Material tool.


    Figure 13.
  2. Click anywhere on the pipe geometry.
    The entire geometry is highlighted.


    Figure 14.
  3. In the microdialog, select Water from the Material drop-down menu.
  4. On the guide bar, click to execute the command and exit the tool.
  5. Save the model.

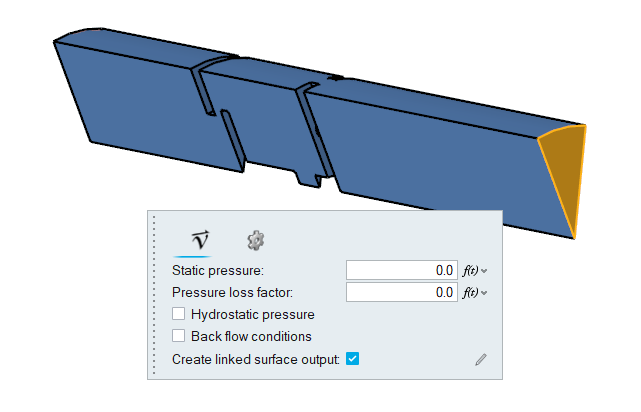
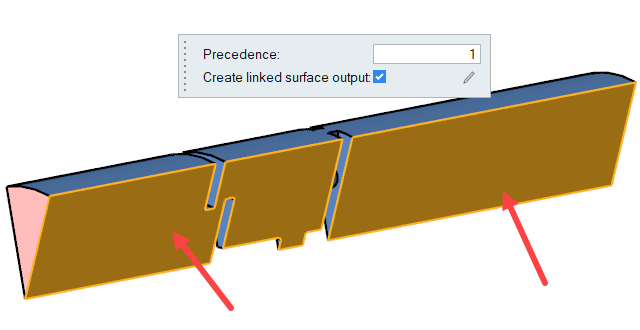
Define Flow Boundary Conditions

In this step, you will assign the boundary conditions for the inlet, outlet and the symmetry faces.
  1. From the Flow ribbon, Pressure tool group, click the Stagnation Pressure tool.


    Figure 15.
  2. In the modeling window, click on the inlet surface, as shown in Figure 16.
  3. In the microdialog, enter a value of 1 N/m2 for the Stagnation pressure.
  4. Click the Multiplier function drop-down and select the function Inlet Pressure from the list.


    Figure 16.
  5. Click the Turbulence icon the microdialog, set the Turbulence input type to Viscosity Ratio, and the enter a value of 10 for the Turbulence viscosity ratio.


    Figure 17.
  6. On the guide bar, click to execute the command and remain in the tool.
  7. In the Boundaries legend, right-click on Stagnation pressure and rename it to Inlet then press Enter.
  8. Click the Outlet tool.


    Figure 18.
  9. Click the outlet surface shown in the figure below.


    Figure 19.
  10. On the guide bar, click to execute the command and exit the tool.
  11. Click the Symmetry tool.


    Figure 20.
  12. Select the two surfaces shown in the figure below.


    Figure 21.
  13. On the guide bar, click to execute the command and remain in the tool.
  14. In the Boundaries legend, rename Symmetry to Front_symmetry.
  15. Rotate the model and select the other two symmetry faces.


    Figure 22.
  16. On the guide bar, click to execute the command and remain in the tool.
  17. In the Boundaries legend, rename Symmetry to Back_symmetry.
  18. Save the model.

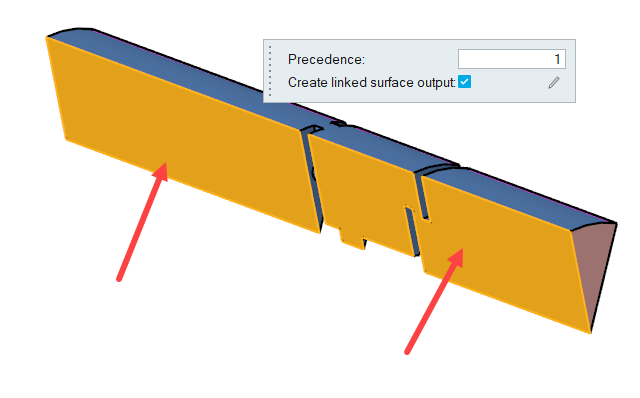
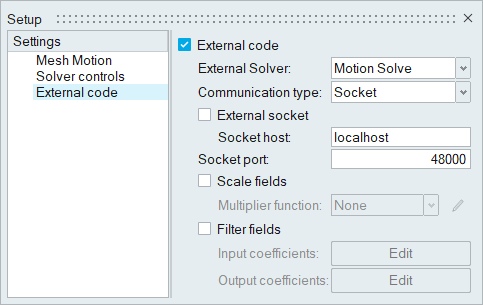
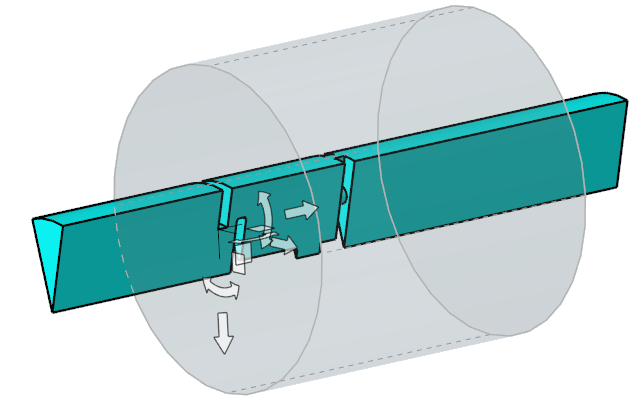
Set Up Motion

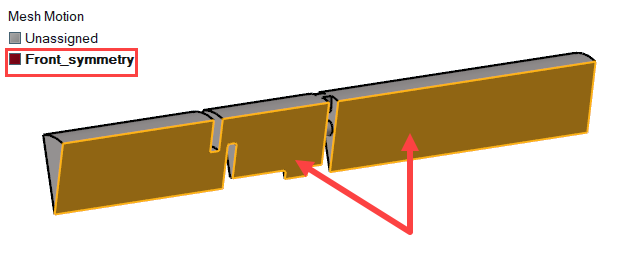
In this step, you will activate the mesh motion and define the rigid body motion for the valve wall. Then, you will define the mesh displacement boundary conditions for the symmetry surfaces.

Define the Mesh Motion Type

  1. From the Motion ribbon, click the Settings tool.


    Figure 23.
  2. In the Setup dialog, change the Mesh motion to Arbitrary.


    Figure 24.
  3. Click the External code setting and activate the External code option.
  4. Set the External Solver to MotionSolve and the Communication type to Socket.
  5. Deactivate the External socket option and set the Socket host to localhost.
  6. Set the Socket port to 48000.


    Figure 25.
  7. Close the dialog.

Define the Mesh Displacement Boundary Conditions

  1. From the Motion ribbon, click the Planar Slip tool.


    Figure 26.
  2. Select the two front symmetry surfaces shown Figure 27.
  3. In the Mesh Motion legend, rename Planar Slip to Front_symmetry by double-clicking on the name.


    Figure 27.
  4. On the guide bar, click to execute the command and remain in the tool.
  5. Rotate the model and select the two back symmetry faces.
  6. In the Mesh Motion legend, rename Planar Slip to Back_symmetry.
  7. On the guide bar, click to execute the command and exit the tool.
  8. Click the External Surface tool.


    Figure 28.
  9. On the guide bar, make sure the Surfaces selector is active.
  10. Right-click in the modeling window and go to Select > Advanced Select > By Boundaries > Default Wall.
  11. Now that all the wall surfaces are highlighted, isolate the selected surfaces either by pressing the I key, or by right-clicking in the modeling window and selecting Isolate.
  12. Zoom in on the valve region and select all the valve wall surfaces using the window selection method.


    Figure 29.
  13. In the microdialog, set the Coupling direction to Both and enter Model-Shutter Body as the name of the Rigid body.
    Note: The name of the rigid body specified here should match the name of the rigid body in the MotionSolve model.


    Figure 30.
  14. In the External Code Surfaces legend, rename the External Surface to Valve wall.
  15. On the guide bar, click to execute the command and exit the tool.
  16. Turn on the display of all surfaces and save the model.

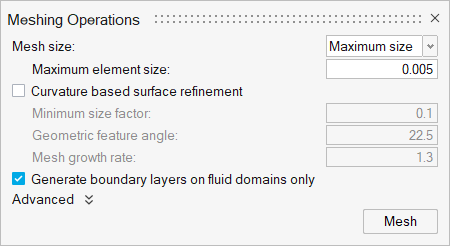
Generate the Mesh

In this step, you will define the mesh controls and then generate the mesh.

Define the Zone Mesh Controls

The zone mesh controls allow you to define a local volume mesh size for specific regions using standard shaped zones like cylindrical, spherical, and cuboidal zones.
  1. From the Mesh ribbon, Zones tool group, click the Cylinder tool.


    Figure 31.
  2. In the modeling window, hover the mouse around the point shown in the figure below. When the preview cylinder zone is parallel to the axis of the pipe, click on the model near the point shown below.
    This point will be the center of the front face of the cylinder. In the next few steps you will edit the co-ordinates of this point manually.


    Figure 32.
  3. Move the mouse cursor away from the center and then click again.
    A preview of the zone should be displayed on the screen along with the manipulator. The manipulator allows you to modify the location and orientation of the zone.


    Figure 33.
  4. Click the center of the manipulator and enter the following coordinates for the center (-0.06, 0.02, 0)


    Figure 34.
  5. Double-click on the cylindrical surface of the zone and enter 0.022 m as the radius of the cylinder.


    Figure 35.
  6. Double-click on the base of the cylinder and enter 0.1 m as the height of the cylinder.


    Figure 36.
  7. Click anywhere in the empty space in the modeling window.
  8. Enter a value of 0.0015 m for the mesh size in the microdialog.
  9. In the Refinement zones legend, rename the zone to Valve region mesh refinement.


    Figure 37.
  10. Save the model.

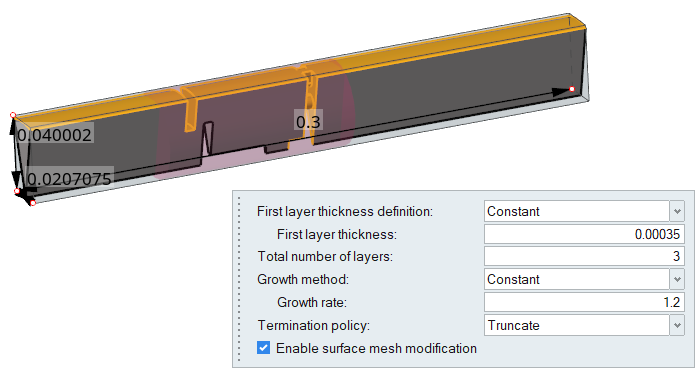
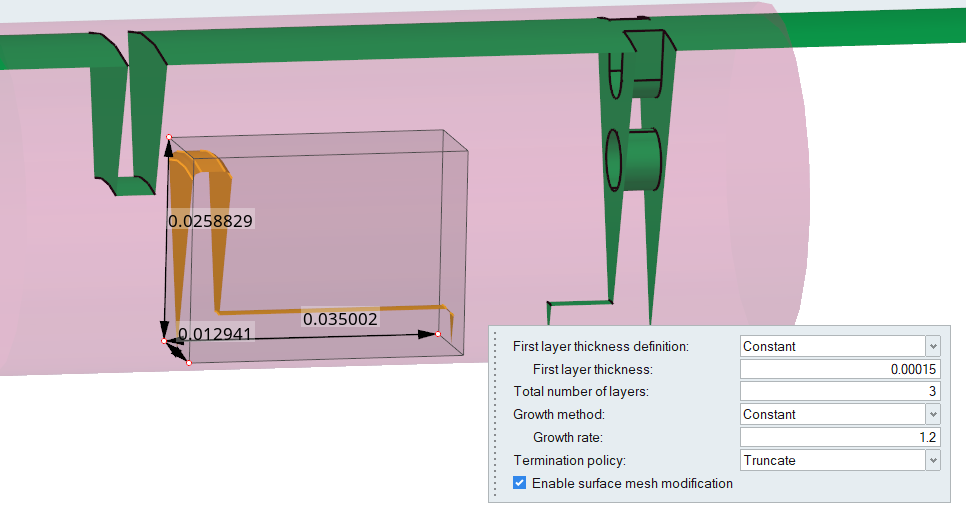
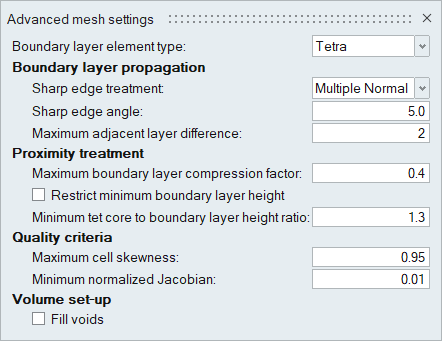
Define the Boundary Layer Controls

  1. From the Mesh ribbon, click the Boundary Layer tool.


    Figure 38.
  2. Right-click in the modeling window and go to Select > Advanced Select > By Boundaries > Default Wall.
    All the wall surfaces should be highlighted and a dialog for BL specification appears.
  3. Enter the following values in the dialog:
    1. First layer thickness: 0.00035
    2. Total number of layers: 3
    3. Growth method: Constant
    4. Initial growth rate: 1.2
    5. Termination policy: Truncate
    6. Activate Enable surface mesh modification.


    Figure 39.
  4. In the BL Controls legend, rename the BL control to Pipe walls BL.
  5. On the guide bar, click to execute the command and remain in the tool.
  6. In the next few steps, you will define the boundary layer mesh control for the valve walls. For convenience, hide the front and back symmetry faces.
  7. Select the valve wall surfaces using the box selection method.
  8. In the dialog that appears, enter the following values for the BL specification:
    1. First layer thickness: 0.00015
    2. Total number of layers: 3
    3. Growth method: Constant
    4. Initial growth rate: 1.2
    5. Termination policy: Truncate
    6. Activate Enable surface mesh modification.


    Figure 40.
  9. In the BL Controls legend, rename the BL control to Valve walls BL.
  10. On the guide bar, click to execute the command and exit the tool.
  11. Click the drop-down next to the Mesh Controls tool set and select Advanced.


    Figure 41.
  12. In the Advanced mesh settings dialog, change the Boundary layer element type to Tetra then close the dialog.


    Figure 42.
  13. Turn on the display of all the surfaces and save the model.

Generate the Mesh

  1. From the Mesh ribbon, click the Volume tool.


    Figure 43.
  2. In the Meshing Operations dialog, set the Mesh size option to Maximum size and set the Maximum element size to 0.005.
  3. Deactivate Curvature based surface refinement.
  4. Click Mesh to generate the mesh.


    Figure 44.

    Once the meshing process has started, the Run Status dialog appears and the application moves to the Solution ribbon.

  5. Once the meshing is completed, close the Run Status dialog.

Compute the Solution

Define Nodal Outputs

  1. From the Solution ribbon, click the Field tool.


    Figure 45.
  2. In the Field Outputs dialog, set the Time step interval to 1 for the Solution variables.


    Figure 46.

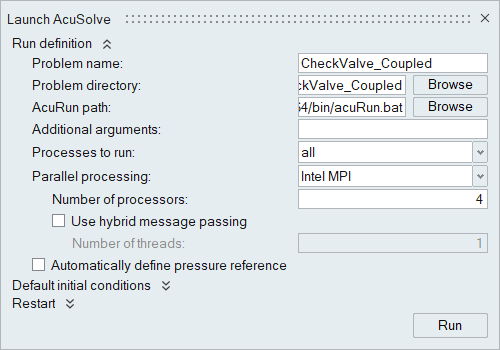
Run AcuSolve

  1. From the Solution ribbon, click the Run tool.


    Figure 47.
  2. Set the Parallel processing option to Intel MPI.
  3. Optional: Set the number of processors to 4 or 8 based on availability.
  4. Deactivate the Automatically define pressure reference option.
  5. Leave the remaining options as default and click Run to launch AcuSolve.


    Figure 48.
    The Run Status dialog opens. Once the run is complete, the status is updated and you can close the dialog.

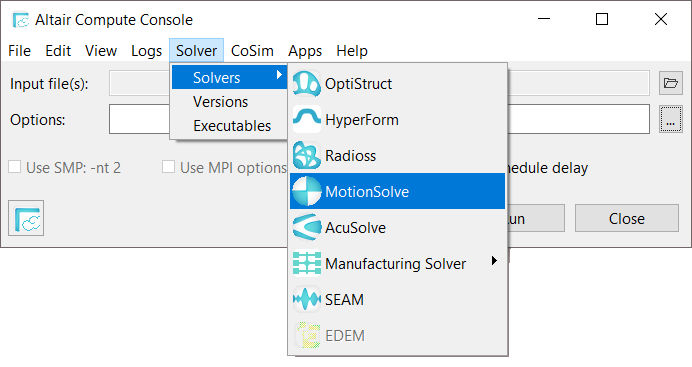
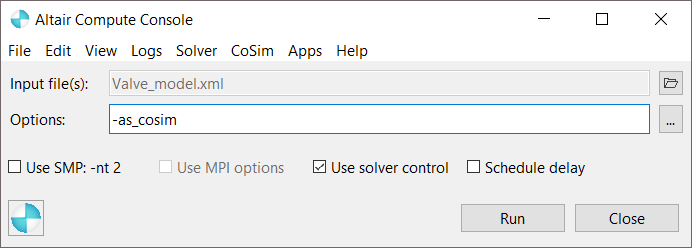
Run MotionSolve

  1. Run Start > All Programs > Altair <version> > Compute Console.
  2. Select Solver > MotionSolve from the menu bar.


    Figure 49.
  3. Click besides the Input file(s) field, browse to the location where you saved Valve_model.xml, and open it
  4. For Options, type -as_cosim to indicate coupling between MotionSolve and AcuSolve.


    Figure 50.
  5. Click Run to start MotionSolve.

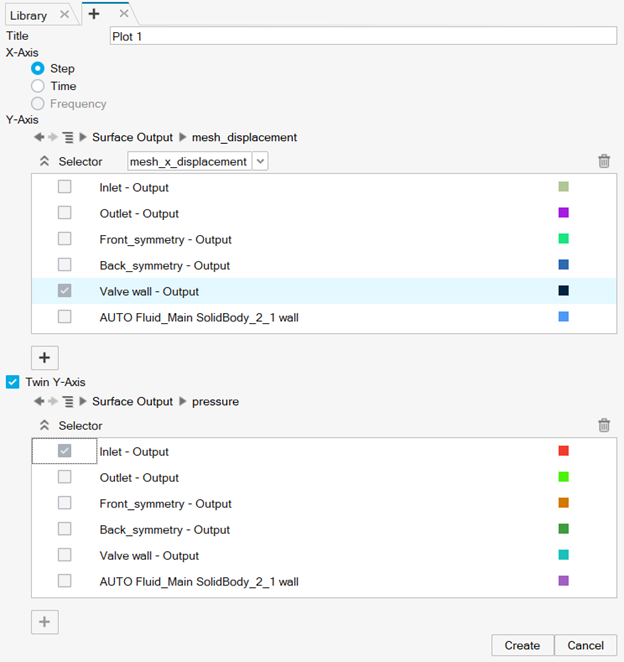
Monitor the Results

  1. From the Solution ribbon, click the Plot tool.


    Figure 51.
  2. Click next to the Library tab.
  3. Keep the X-axis set to Step. For the Y-axis, click the tree browser and select mesh_displacement under Surface Output.
    mesh_x_displacement is selected by default for the coordinate direction.
  4. Check the box for Valve wall - Output under Selector.
  5. Check the box for Twin Y-Axis.
  6. Click the tree browser for the second Y-axis and select pressure under Surface Output.
  7. Check the box for Inlet - Output under Selector.


    Figure 52.
  8. Click Create.


    Figure 53.
    Note: The valve motion lags behind the pressure changes at the inlet. Note also the spike around the 37th time step. This represents the collision of the valve stem with the stop and the subsequent rebound of the valve.

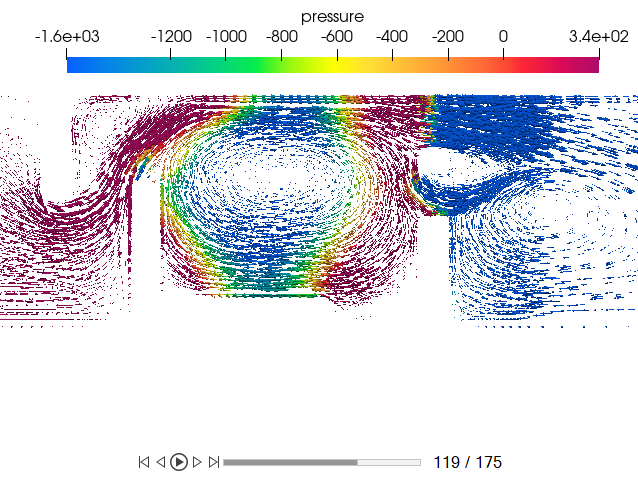
Post-Process the Results with HW-CFD Post

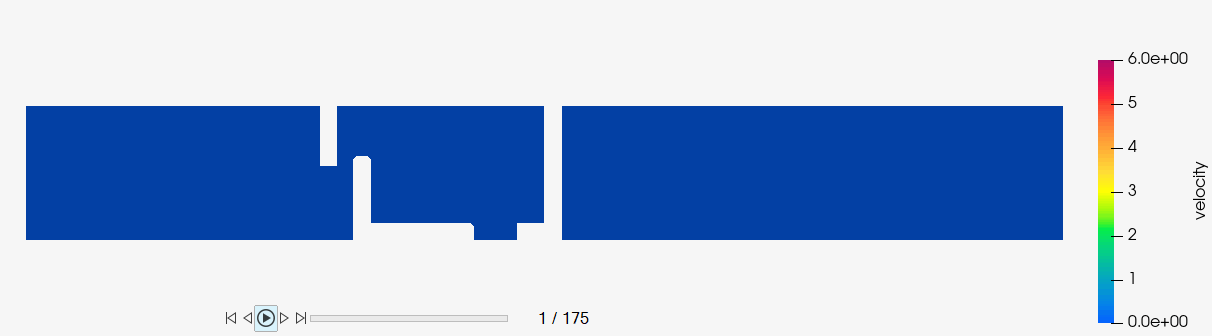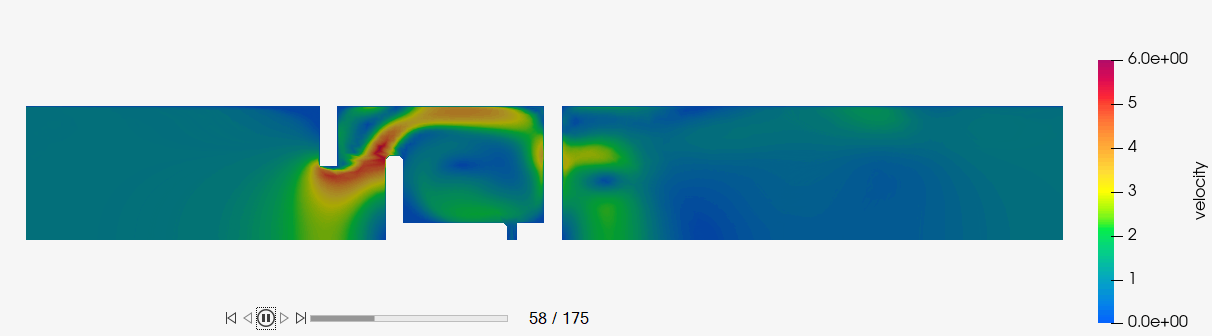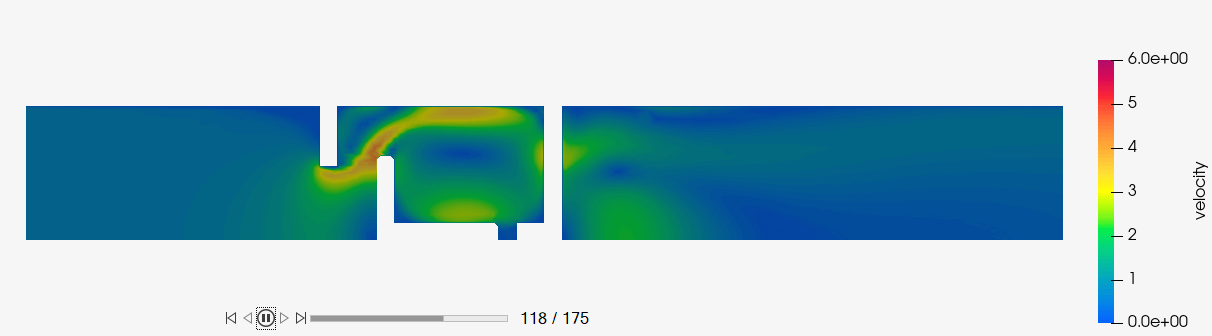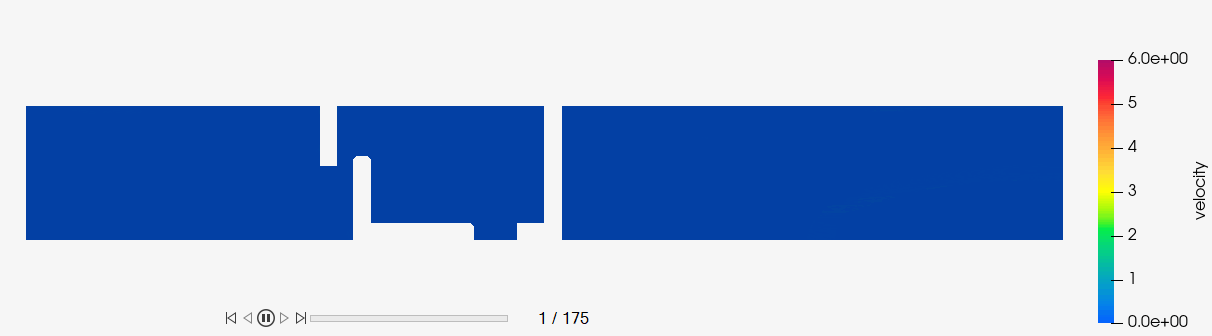
Create an Animation of Velocity Magnitude

  1. Once the solution is completed, navigate to the Post ribbon.
  2. From the menu bar, click File > Open > Results.
  3. Select the AcuSolve log file in your problem directory to load the results for post-processing.
    The solid and all the surfaces are loaded in the Post Browser.
  4. Click the Top face on the View Cube to align the model.


    Figure 54.
  5. In the Post Browser, right-click on Front_symmetry and select Isolate.
  6. Right-click on Front_symmetry once more and select Edit.
  7. In the display properties microdialog, set the display to velocity.
  8. Activate the Legend toggle and set the max velocity to 6.0.
  9. Click and set the Colormap Name to Rainbow Uniform.


    Figure 55.
  10. Click on the guide bar.
  11. Click at the bottom of the modeling window to view a live animation of the flow.


    Figure 56.
  12. Save the animation.
    1. Go to File > Screen Capture > Advanced Capture.
    2. Click on the toolbar.
    3. Uncheck Include mouse cursor.
    4. Set the frame rate to 50.
    5. Click on the toolbar then drag over the area you want to record.
    6. Click to start recording and the same button to stop recording.
    7. Name the file and save it.

Display Pressure Contours and Velocity Vectors on a Section Cut

  1. Right-click in the modeling window and select Show All.
  2. Click the Slice Planes tool.


    Figure 57.
  3. Select the plane perpendicular to the z-axis.
  4. Make sure the View Cube is aligned with the Top face.


    Figure 58.
  5. Click in the slice plane microdialog.
  6. Turn off the Display in the Contour tab of the display properties microdialog.


    Figure 59.
  7. Click the Vector Display tab.
  8. Turn the Display on, set the variable to velocity, and the value to 0.001.
  9. Set the Coloring to pressure.
  10. Activate the Legend toggle and click to reset the range.
  11. Click , set the Legend location to Upper Center, the Legend orientation to Horizontal, and the Colormap Name to Rainbow Uniform.


    Figure 60.
  12. Click on the guide bar.
  13. In the Post Browser, right-click on Slice Plane 1 and select Isolate.


    Figure 61.

Summary

In this tutorial, you learned the basic workflow to set up a co-simulation using AcuSolve and MotionSolve. The tutorial introduced you to the steps involved in setting up external code communication between AcuSolve and MotionSolve using HyperWorks CFD, and then running the simulation and post-process the results using HyperWorks CFD Post. You also learned how to create a vector plot on an existing contour plot on a cut plane.