ACU-T: 7000 Parametric Optimization with AcuSolve

This tutorial provides instructions for setting up, solving, and viewing results for a parametric optimization problem in AcuSolve. The parametric studies enable you to specify one or more conditions that may vary, such as a sweep over a range of inlet mass flow boundary conditions. The range and frequency of the parameter controlling the mass flow is selected either by simply specifying the desired values or having the program compute suitable values automatically. Several parameters can be used in parametric studies, for instance, controlling the inlet mass flow, the impeller rotational speed, and blade angles of a fan problem. The model used for this tutorial consists of a sphere immersed in a fluid flow. The surface of the sphere is kept hot from an internal heat source. The fluid flow removes the heat from the sphere surface, thus causing the temperature of the fluid to rise. The simulation is run with various values of temperature at the fluid inlet to determine the conditions which result in the outlet temperature closest to a desired value.

The basic steps in a CFD simulation have been discussed in the earlier tutorials. The following additional capabilities of AcuSolve are introduced in this tutorial:
  • Setting up a parametric optimization problem in AcuSolve
  • Post-processing a parametric optimization problem

In this tutorial, you will:

  • Analyze the problem
  • Import the HyperMesh model database
  • Set general simulation parameters and solver settings
  • Set material model parameters and nodal initial conditions
  • Set up the optimization study parameters
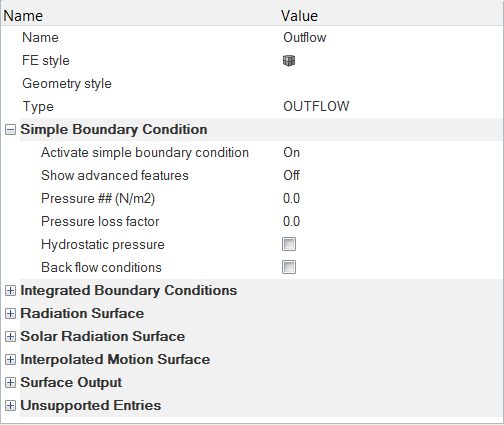
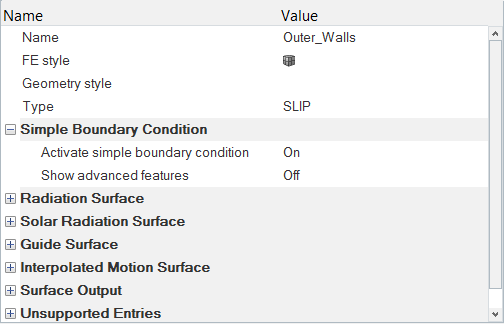
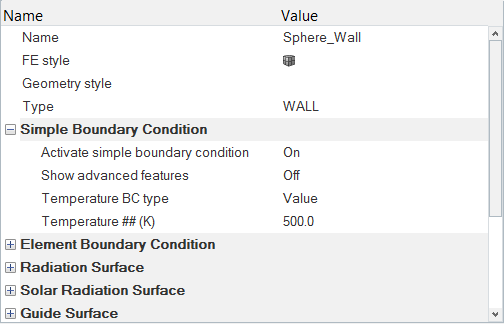
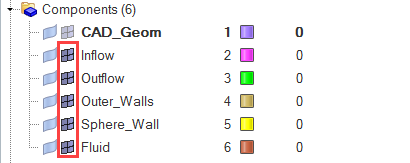
  • Assign surface boundary conditions and material properties
  • Run AcuSolve
  • Monitor the solution with AcuProbe

Prerequisites

Prior to starting this tutorial, you should have already run through the introductory HyperWorks tutorial, ACU-T: 1000 HyperWorks UI Introduction, and have a basic understanding of HyperMesh and AcuSolve. To run this simulation, you will need access to a licensed version of HyperMesh and AcuSolve.

Prior to running through this tutorial, click here to download the tutorial models. Extract ACU-T7000_ParametricOptimization.hm from HyperMesh_tutorial_inputs.zip.

Since the HyperMesh database (.hm file) contains meshed geometry, this tutorial does not include steps related to geometry import and mesh generation.

Analyze the Problem

Figure 1 shows the schematic of the problem that will be solved in this tutorial. The fluid enters the channel from the left side, and flows around the sphere immersed in the channel. The sphere surface is maintained at a constant temperature of 500 K. The fluid flow rate is set to be constant. The fluid inlet temperature is varied over a range of values which are a combination of specified values and those chosen by the program on basis of a set of parameters. The fluid model used for this problem is a hypothetical fluid material.


Figure 1.

The inlet temperature here is what is known as the “design variable” for the problem. A target value for outlet temperature is specified, and the desired inlet temperature is the value at which the outlet temperature is closest to the target outlet temperature. The difference between the target outlet temperature and the actual outlet temperature is what is known as the “response variable” for the problem. Since the objective of the problem is to minimize the difference between the outlet temperature and the target outlet temperature, this problem is a “minimization” problem.

Optimization

Optimization, in simple terms, is the process of selecting a best input from a set of available alternatives. Almost all engineering problems today are aimed at optimizing something. Airfoil designers are always trying to come up with new airfoil designs with better lift and low drag. Heat exchanger component designers want to maximize the surface heat flux while also minimizing the pressure drop through the exchanger.

AcuSolve offers you two options to setting up an optimization study: design optimization and parametric studies. Design optimization enables you to optimize an objective function subject to certain constraints and satisfaction of flow equations.

Parametric studies enables you to specify one or more conditions that may vary, such as a sweep over a range of inlet mass flow boundary conditions. In parametric studies, these control parameters vary according to a specified pattern. For example, the range and frequency of the parameter controlling the mass flow is selected either by simply specifying the desired values or having the program computing suitable values automatically. Several parameters can be used in parametric studies, for instance, controlling the inlet mass flow, the impeller rotational speed, and blade angles of a fan problem. Perhaps you want to evaluate the pressure rise and torque of the fan; these outputs are called "response variables". The parameters controlling the run conditions are called "variables" or "design variables". The nomenclature is similar to the optimization problems.

Both design optimization and parametric studies manage analyses where,
  1. the geometry is allowed to change (geometric design and shape optimization) and/or
  2. internal parameters, such as the inlet flow rate or viscosity, are allowed to change (design of experiments and quantified optimization).

A minimization problem where a local minimum is sought can be stated as:

                Minimize,        objective(U,Y)
                        subject to            constraints(U,Y)

Here, U is the flow solution variables and Y is a vector of control parameters, called Design Variables (DVs), that determines the shape of an object or a flow parameter. The objective(s) and constraint(s) are specified by you. A maximization problem is the same as above, but Minimize is replaced with Maximize.

Optimization Solution Sequence

The design optimization may be considered as a sequence of cases, where each case first runs the optimizer and updates the design variables and then solves the flow equations for a number of time steps until convergence. Sample data is gathered at the end of each time step.

The optimizer solution consists of:
  1. Constructing the response surface from the set of samples.
  2. Running the optimizer on the response surface.
  3. Updating the design variables.


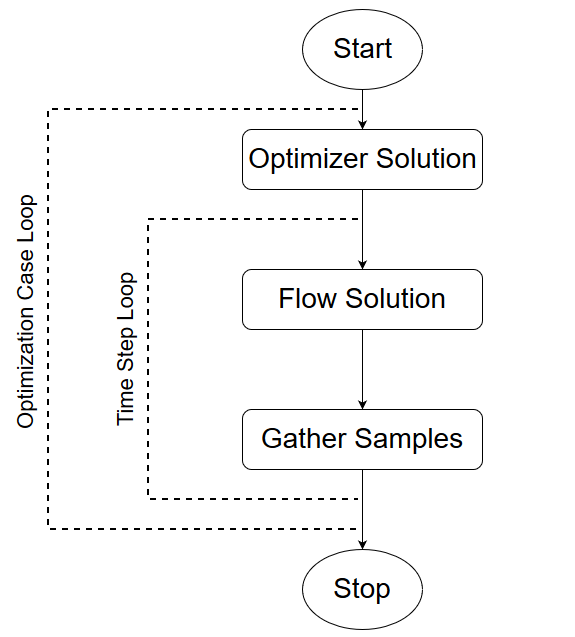
Figure 2.

Open the HyperMesh Model Database

  1. Start HyperMesh and load the AcuSolve user profile.
    Refer to the HM introductory tutorial, ACU-T: 1000 HyperWorks UI Introduction, to learn how to select AcuSolve from User Profiles.
  2. Click the Open Model icon located on the standard toolbar.
    The Open Model dialog opens.
  3. Browse to the directory where you saved the model file. Select the HyperMesh file ACU-T7000_ParametricOptimization.hm and click Open.
  4. Click File > Save As.
    The Save Model As dialog opens.
  5. Create a new directory named ParametricOptimization and navigate into this directory.
    This will be the working directory and all the files related to the simulation will be stored in this location.
  6. Enter ParametricOptimization as the file name for the database, or choose any name of your preference.
  7. Click Save to create the database.

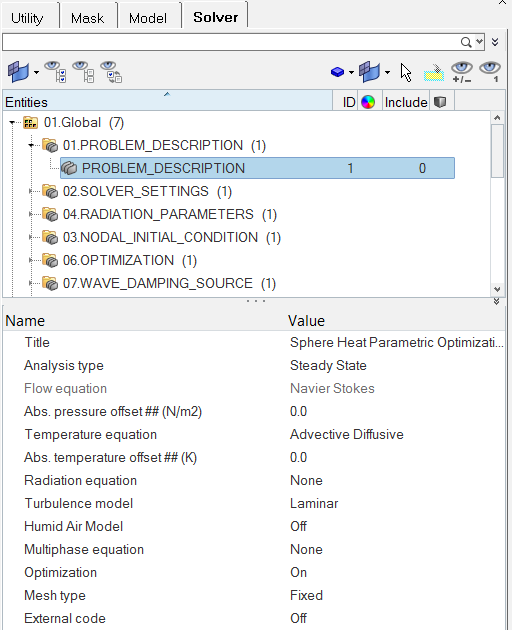
Set the Global Simulation Parameters

Set the Analysis Parameters

In next steps, you will set parameters that apply globally to the simulation.

  1. Go to the Solver Browser, expand 01.Global, then click PROBLEM_DESCRIPTION.
  2. In the Entity Editor, change the Temperature equation to Advective Diffusive.
  3. Set Optimization to On.


    Figure 3.

Specify the Solver Settings

  1. In the Solver Browser, expand the 02.SOLVER_SETTINGS group then click SOLVER_SETTINGS to open it in the Entity Editor.
  2. Set the Min optimization cases to 10.
  3. Set the Max optimization cases to 50.
  4. Set the Optimization convergence tolerance to 1e-05.
    The above three parameters are new parameters specific to an optimization setup in AcuSolve. The minimum and maximum optimization cases are the minimum and maximum number of unique input cases that will be solved. The optimization convergence tolerance checks for the change in results on a case-by-case basis. The optimization stops when either the optimization convergence tolerance is achieved, or the specified number of maximum optimization cases is reached.
  5. Set Max time steps to 10.
  6. Set the Convergence tolerance to 0.0001.
    The Min and Max time steps are the minimum and maximum number of time steps solved for each case. The solver moves on to the next case when either the convergence tolerance is achieved, or the specified number of maximum time steps is reached.
  7. Set the Relaxation factor to 0.0.
  8. Check that the Flow, Temperature, and Design Optimization flags are set to On and the Temperature flow flag is set to Off.


    Figure 4.

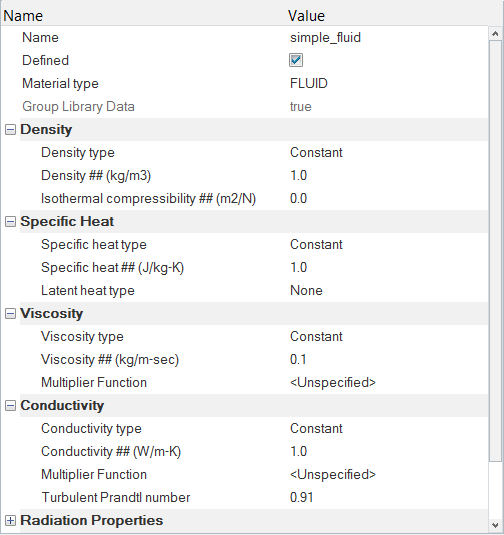
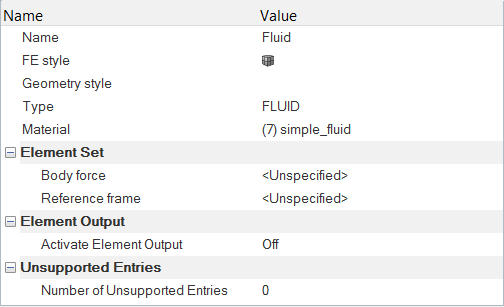
Set Material Model Parameters

In the next steps, you will create a new custom material and assign relevant material properties to it.

  1. In the Solver Browser, expand 02.Materials the right-click on FLUID and select Create.
  2. Rename the material as simple_fluid in the Entity Editor.
  3. Set the Density value to 1.0 kg/m3.
  4. Set the Viscosity value to 0.1 kg/m-sec.
  5. Set the Conductivity value to 1.0 W/m-K.


    Figure 5.
  6. Save the model.

Set Up the Optimization Parameters

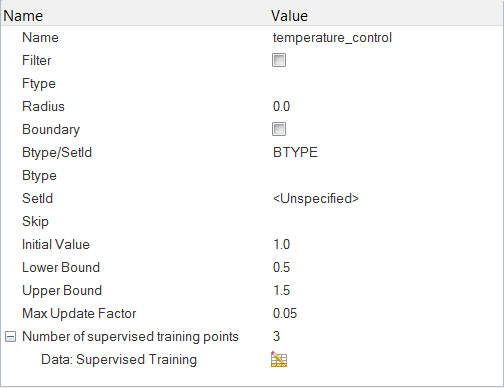
Define the Design Variable

  1. In the Solver Browser, right-click on 10.Optimization and select Optimization > DESIGN_VARIABLES from the context menu.
  2. Rename the variable as temperature_control in the Entity Editor.
  3. Set the Initial Value to 1.0.
  4. Set the Lower Bound to 0.5.
  5. Set the Upper Bound to 1.5.
  6. Set the Max Update Factor to 0.05.
    The lower and upper bound values define the range of values between which the design variable can be set. The initial value is the value of the design variable that will be used for the first case, or the initial condition. The maximum update factor controls the maximum change allowed in the design variable value from one case to the next.
  7. Set the Number of supervised training points to 3.
  8. Click inside the value field for the newly created Data: Supervised Training row.
    The Number of supervised training points dialog opens. The number of available rows is equal to the number of points specified in the previous step.
  9. Enter 1.0 in row 1, 0.9 in row 2, and 0.8 in row 3 then click Close.
    The Supervised Training parameter is used to enforce AcuSolve to use the listed design variable values for as many cases as there are values in the list. After the list is exhausted, optimization control takes over. It is advisable to provide at least three values for Supervised Training as it helps the solver develop a pattern, streamlining the process of selecting the values for design variable for succeeding runs.


    Figure 6.

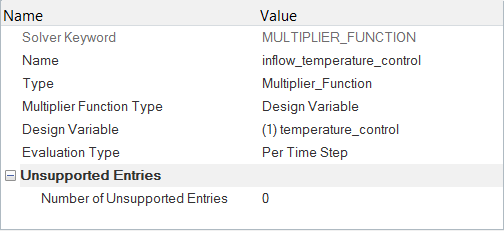
Create a Multiplier Function for the Design Variable

In AcuSolve, multiplier functions are used to scale values of certain parameters at runtime. For example, viscosity of a fluid may vary with temperature. Or inflow rate or temperature may vary over time.

Multiplier functions can also be used to scale the values of the design variables between cases. In quantity optimization, the design variables are linked with the desired quantities in AcuSolve through multiplier functions.

  1. In the Solver Browser, right-click on 05.Multiplier_Function and select Create from the context menu.
  2. Rename the function as inflow_temperature_control in the Entity Editor.
  3. Change the Multiplier Function Type to Design Variable.
  4. Click in the value field next to Design Variable, click the Designvar collector, select temperature_control from the appearing dialog, then click OK.


    Figure 7.

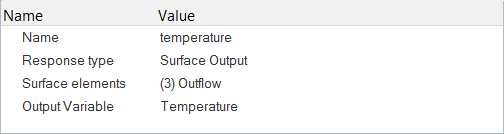
Define Response Variables

Response variables are the building blocks for deriving objective functions and constraints. Examples include: drag, lift, force in an arbitrary direction, total volume, pressure drop, total pressure, uniformity index on temperature, max speed, etc. In other words, response variables are functions of the flow solution (via output mechanism), the design variables, and/or other response variables.

The most basic response variables are functions of the flow solution, extracted from the SURFACE_OUTPUT and ELEMENT_OUTPUT. More complex response variables can be derived from these basic response variables using expressions. An example of this is demonstrated in the following steps.

  1. In the Solver Browser, right-click on 10.Optimization and select Optimization > RESPONSE_VARIABLES from the context menu.
  2. Rename the variable as temperature in the Entity Editor.
  3. Repeat the above steps to create three new response variable entries and rename them to:
    1. target_temperature
    2. temperature-target_temperature
    3. (temperature-target_temperature)^2
  4. Click on temperature. In the entity editor,
    1. Change the Response type to Surface Output.
    2. Click in the value field next to Surface Elements, click the Component collector, select Outflow from the appearing dialog, and click OK.
    3. Set the Output variable to Temperature.
    This response variable will extract the surface integrated value of the temperature variable from the outflow surface.


    Figure 8.
  5. Click on target_temperature. In the Entity Editor,
    1. Change the Response type to Constant.
    2. Set the Value to 325.0.
    This response variable is set to a constant value or 325 K.
  6. Click on termperature-target_temperature. In the Entity Editor,
    1. Change the Response type to Subtraction.
    2. Click on the value field for the Data: Response variables row.
    3. In the dialog that opens, click inside row 1 then click on the Optiresponse collector.
    4. In the Select Optiresponse dialog, select temperature from the list and click OK.
    5. Similarly, select target_temperature for row 2.
    6. Click Close to exit the dialog.
    This response variable will extract the difference between the two response variables, temperature and target_temperature.
  7. Click on (termperature-target_temperature)^2. In the Entity Editor,
    1. Change the Response type to Multiplication.
    2. Click on the value field for the Data: Response variables row.
    3. In the dialog that opens, click inside row 1 then click on the Optiresponse.
    4. In the Select Optiresponse dialog, select temperature-target_temperature from the list and click OK.
    5. Similarly, select temperature-target_temperature for row 2.
    6. Click Close to exit the dialog.

    This response variable will return the squared value of the response variable, temperature-target_temperature.

Define the Objectives

It was mentioned earlier that the response variables are the building blocks for deriving objective functions and constraints. In this section, you will define a new objective and link an existing response variable to that objective entity.

The objective of an optimization problem is usually minimization or maximization of a response variable. In this problem, the objective is to minimize the difference between the actual and the target outflow temperature. In the next few steps, you will create and define the objective accordingly.

  1. In the Solver Browser, expand Optimization > OBJECTIVES then click on objective1.
  2. Rename the objective as find_inflow_temperature in the Entity Editor.
  3. Check that the Objective Type is set to Minimize.
  4. Set the Response variable to (temperature-target_temperature)^2 by clicking in the value field next to Response variable then selecting the correct response variable from the Select Optiresponse dialog.
    Note: If there are any constraints in your problem, you can define them similarly under the Constraints group.

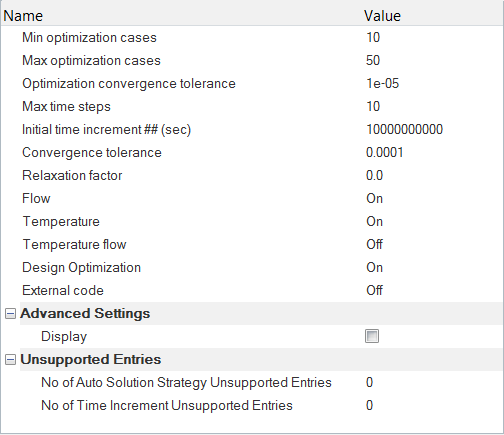
Set Up Optimization Controls

In the Optimization command, you will link all the defined objectives and constraints to define the optimization problem. There are no constraints defined for this problem, but if there are any, they should be defined first under the Constraints entry in the Data Tree.

  1. In the Solver Browser, expand 01.Global then click on 06.OPTIMIZATION.
  2. In the Entity Editor, verify that the Objective is set to find_inflow_temperature.
  3. If there are any constraints in your problem, you can set the value for the Number of Constraints field accordingly and then define the constraints.
  4. Verify that the Optimizer convergence tolerance is set to 1e-4.

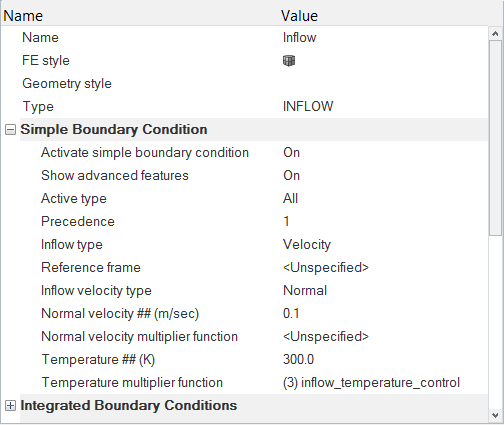
Assign Boundary Conditions and Material Properties

By default, all components are assigned to the wall boundary condition. In this step, you will change them to the appropriate boundary conditions and assign material properties to the fluid volumes.
  1. In the Solver Browser, expand Volumes
  2. Click Fluid. In the Entity Editor,
    1. Change the Type to FLUID.
    2. Select simple_fluid as the Material.


    Figure 9.
  3. Click Inflow. In the Entity Editor,
    1. Change the Type to INFLOW.
    2. Turn On the Show advanced features field.
    3. Set the Normal velocity to 0.1 m/sec.
    4. Set the Temperature to 300 K.
    5. Set the Temperature multiplier function to inflow_temperature_control.


    Figure 10.
  4. Click Outflow. In the Entity Editor, change the Type to OUTFLOW.


    Figure 11.
  5. Click Outer_Walls. In the Entity Editor, change the Type to SLIP.


    Figure 12.
  6. Click Sphere_Wall. In the Entity Editor,
    1. Change the Type to WALL.
    2. Change the Temperature BC type to Value.
    3. Set the Temperature to 500 K.


    Figure 13.
  7. Save the model.

Compute the Solution and Review the Results

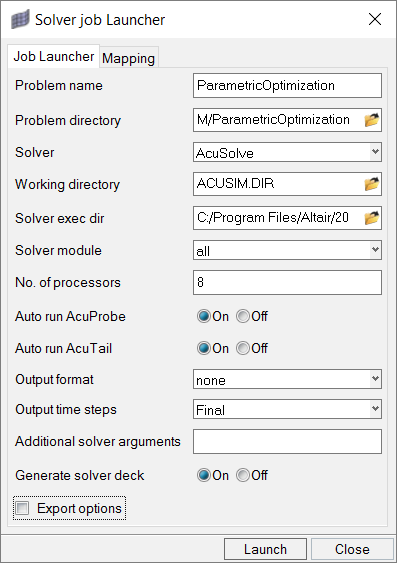
Run AcuSolve

In this step, you will launch AcuSolve directly from HyperMesh and compute the solution.

  1. In the Model Browser, ensure that the visibility of the mesh for all collectors to be exported for AcuSolve are activated. In this case, display for all the collectors – Fluid, Inflow, Outflow, Sphere_Wall, and Outer_Walls – should be activated.


    Figure 14.
  2. Click on the ACU toolbar.
    The Solver job Launcher dialog opens.


    Figure 15.

    For this case, the default settings will be used. You may choose to change the number of processors to allow AcuSolve to run using more processors (4 or 8), if available. HyperMesh will generate the required solver input files and launch AcuSolve. AcuSolve will calculate the steady state solution for this problem.

  3. Verify that Auto run AcuProbe is On.
    This will open an AcuProbe dialog which will let you monitor the solution progress.
  4. Click Launch to start the solution process.
    As the solution progresses, an AcuTail dialog opens where solution progress is reported. An AcuSolve Control dialog also opens from which you can control the solution process. In this dialog you have options to stop the solution or generate the output files at the end of the current time step.
    You'll notice AcuSolve prints the case number before beginning the solution for the case. The Case-Step number is reset to 1 when AcuSolve moves to a new case while Time-Step proceeds sequentially.


    Figure 16.

    A summary of the run printed in the AcuTail dialog indicates that AcuSolve has finished running the solution.

    Figure 17.
  5. Close the AcuTail window and save the database to create a backup of your settings.

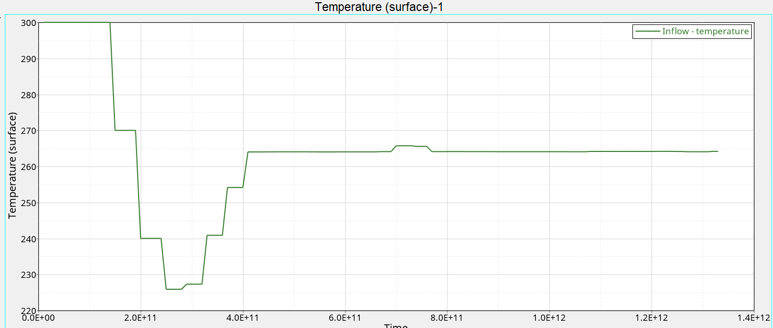
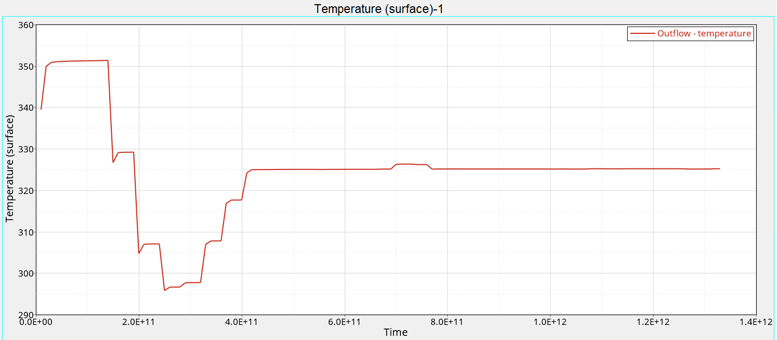
Monitor the Solution with HyperGraph

  1. Click the client selector in the bottom-left corner of the graphics area then select HyperGraph 2D.


    Figure 18.
  2. Once the HyperGraph interface loads, click in the panel area and select the result file from the current working directory.
    In this example, the file to be selected is ParametricOptimization.1.Log.
  3. Make sure that the X Type is set to Time, the Y Type to Temperature (surface), and the Y Request to Inflow.


    Figure 19.
  4. Click Apply.


    Figure 20.

    This plot shows the surface temperature of the inflow surface as the solution progresses.

    In the setup, the inflow temperature is a design variable. At the inflow surface, the temperature varies from case to case in accordance with the values provided to the solver by the optimization program. The first three values of inflow temperature correspond to the values provided in the supervised learning parameter, after which the values are provided by the optimizer. The converged value of the inflow temperature is approximately 264.15 K. This is the value at which the outflow temperature is closest to its target value.

  5. In the Plot Browser, right-click on Inflow-termperature 1 and select Turn off.
  6. To plot the temperature of the outflow surafce, change the Y Request to Outflow then click Apply.


    Figure 21.

    This plot shows the surface temperature of the outflow surface as the solution progresses.

    At the outflow surface, the temperature varies in the beginning of the simulation and ultimately converges to a value close to the target temperature value: 325 K.

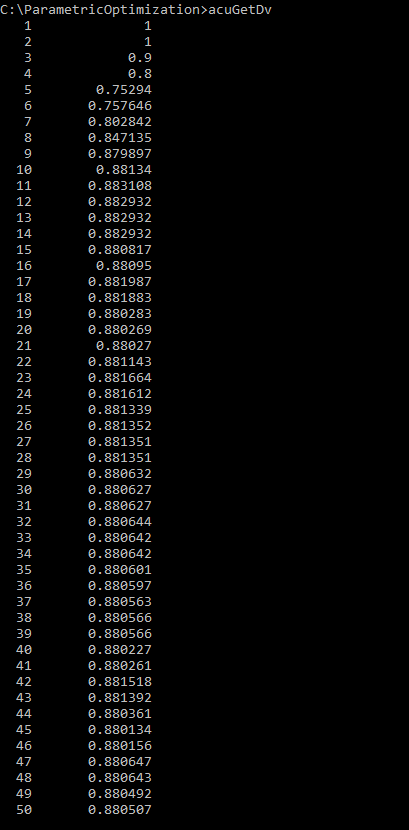
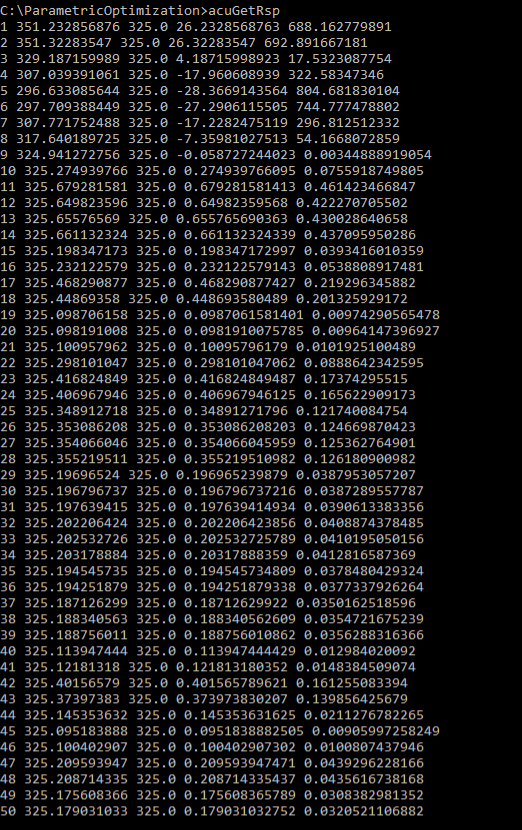
AcuGetDv and AcuGetRsp

AcuSolve provides two post-processing utilities specific to optimization problems, AcuGetDv and AcuGetRsp. AcuGetDv provides the values of the design variables for all the cases included in the solution. AcuGetRsp provides the values of the response variables for all the cases included in the solution.

  1. Start AcuSolve Command Prompt from the Windows Start menu by clicking Start > Altair <version> > AcuSolve Cmd Prompt .
  2. Change the directory to the present working directory using the cd command.
  3. Enter the following command at the prompt:

    acuGetDv

    AcuSolve will print the values of design variables for each case.


    Figure 22.
  4. To print the values of response variables, use the command:

    acuGetRsp

    Note: The order of columns in which the design variables and the response variables are printed by these commands is the order in which they appear in the INP file.


    Figure 23.

Summary

In this AcuSolve tutorial, you successfully set up and solved a parametric optimization problem with AcuSolve. You started the tutorial by creating a database in HyperMesh, importing and meshing the geometry, and setting up the simulation parameters. You defined the design variables, the response variables, and set up the objectives of the problem using the response variables. Once the case was setup, the solution was generated with AcuSolve. HyperGraph was used to visualize the variation of design variables and response variables as the solution progressed through the different cases provided to AcuSolve by the optimization program. You also used the utilities provided in AcuSolve to get the design variables and response variables information for all the cases.