ソース手法とフィールド手法
ソルバー手法は、ソースベース手法とフィールドベース手法に分類できます。これら2種類の手法の主な相違を理解しておくと、応用ごとに適切な解法を把握して選択するうえで効果的です。
離散化
ソース手法では、構造のみを離散化(メッシュ化)し、構造と構造の間の自由空間は離散化しません。フィールド手法では、解領域全体を離散化します。つまり、構造のほか、構造と構造の間の自由空間も離散化します。
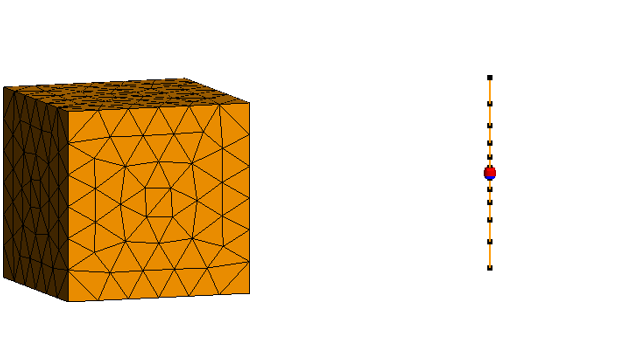
Figure 1. ソースベース手法向けに離散化したダイポールと立方体。

Figure 2. フィールドベース手法向けに離散化したダイポールと立方体。
境界条件
フィールドベース手法では、伝搬する電界に適切な終端(打ち切り)が必要です。したがって、電界に関連するメッシュにも同様の終端が必要です。導波構造や空洞のように、PEC境界によって適切な終端が得られる閉じた領域では、これは問題になりません。一方、Figure 1やFigure 2のような開放した放射の問題では、メッシュを無限遠まで広げる必要があります。この問題を解決するには、メッシュに人為的な吸収領域を設けます。この終端領域(吸収領域)を境界条件と呼びます。ソースベース手法では、メッシュの終端(境界条件)を必要としません。この手法に組み込まれた特殊関数(グリーン関数)によって、無限遠または空間の任意のポイントにおける電界の挙動が自動的に考慮されます。1
解析可能なモデルサイズ
一般的にフィールドベース手法には、解析できるモデルのサイズの面で制限があります。具体的には、モデルの電気的サイズ(波長数)が制限を受けます。この理由は、モデルサイズが大きくなると、メッシュ化して解析するメッシュ要素のボリュームが大きくなることにあります。ソースベース手法では、メッシュ要素で構成した大きいサーフェスのみが解析の対象になるにすぎません。ただし、ソースベース手法では、マルチレベル高速多重極法などの高速化技法の使用を前提としています。また、GPUアクセラレーションの使用量を多くすることにより、フィールドベース手法で解析できるモデルサイズも大きくなる点には注目する必要があります。