Failure Models
| Failure Model | Type | Description |
|---|---|---|
| BIQUAD | Strain failure model | Direct input on effective plastic strain to failure |
| CHANG | Chang-Chang model | Failure criteria for composites |
| CONNECT | Failure | Normal and Tangential failure model |
| EMC | Extended Mohr Coulomb failure model | Failure dependent on effective plastic strain |
| ENERGY | Energy isotrop | Energy density |
| FABRIC | Traction | Strain failure |
| FLD | Forming limit diagram | Introduction of the experimental failure data in the simulation |
| HASHIN 3 4 | Composite model | Hashin model |
| HC_DSSE | Extended Mohr Coulomb failure model | Strain based Ductile Failure Model: Hosford-Coulomb with Domain of Shell-to-Solid Equivalence |
| JOHNSON | Ductile failure model | Cumulative damage law based on the plastic strain accumulation |
| LAD_DAMA | Composite delamination | Ladeveze delamination model |
| NXT | NXT failure criteria | Similar to FLD, but based on stresses |
| PUCK | Composite model | Puck model |
| SNCONNECT | Failure | Failure criteria for plastic strain |
| SPALLING | Ductile + Spalling | Johnson-Cook failure model with Spalling effect |
| TAB1 | Strain failure model | Based on damage accumulation using user-defined functions |
| TBUTCHER | Failure due to fatigue | Fracture appears when time integration of a stress expression becomes true |
| TENSSTRAIN | Traction | Strain failure |
| WIERZBICKI | Ductile material | 3D failure model for solid and shells |
| WILKINS | Ductile Failure model | Cumulative damage law |
Johnson-Cook Failure Model
Where is the increment of plastic strain during a loading increment, the normalized mean stress and the parameters the material constants. Failure is assumed to occur when =1.
Wilkins Failure Criteria
- An increment of the equivalent plastic strain
- Hydrostatic pressure weighting factor
- Deviatoric weighting factor
- Deviatoric principal stresses
- a, and
- The material constants
Tuler-Butcher Failure Criteria
- Fracture stress
- Maximum principal stress
- Material constant
- Time when solid cracks
- Another material constant, called damage integral
Forming Limit Diagram for Failure (FLD)

図 1. Generic Forming Limit Diagram (FLD)
Spalling with Johnson-Cook Failure Model
In this model, the Johnson-Cook failure model is combined to a Spalling model where we take into account the spall of the material when the pressure achieves a minimum value Pmin. The deviatoric stresses are set to zero for compressive pressure. If the hydrostatic tension is computed, then the pressure is set to zero. The failure equations are the same as in Johnson-Cook model.
Bao-Xue Wierzbicki Failure Model
- for solids:
If Imoy=0:
;
If Imoy=1:
- for shells:
;
- Hydrostatic stress
- The von Mises stress
- Third invariant of principal deviatoric stresses
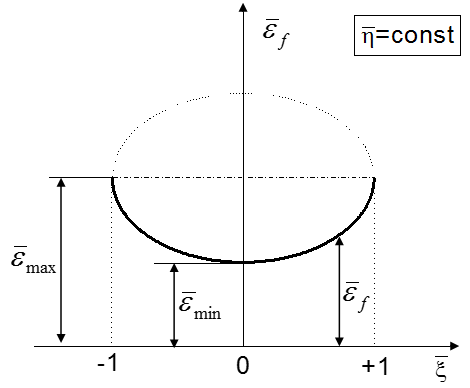
図 2. Graphical Representation of Bao-Xue-Wierzbicki Failure Criteria
Strain Failure Model
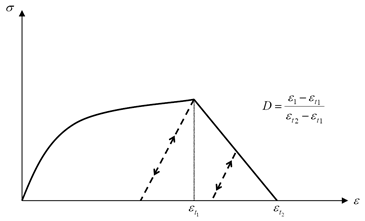
図 3. Strain Failure Model
Energy Density Failure Model
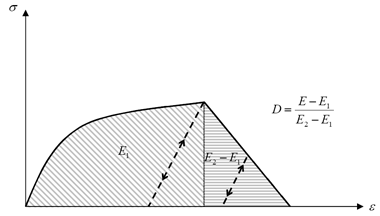
図 4. Strain Failure Model
XFEM Crack Initialization Failure Model
This failure model is available for Shell only.
In /FAIL/TBUTCHER, the failure mode criteria are written as:
- Fracture stress
- Maximum principal stress
- Material constant
- Time when shell cracks for initiation of a new crack within the structure
- Another material constant called damage integral