OS-T: 4090 Manufacturing Constraints of a Composite Structure
In this tutorial you will perform a free-size optimization with manufacturing constraints.
One of the advantages with composite materials is that the structural performance can be controlled precisely by choosing the appropriate ply thickness, ply orientation, stacking sequence, ply materials, and so on. The ability to vary many different parameters provides greater flexibility, but at the same time it is tougher to optimize the part as the number of design variables increases many fold. OptiStruct has the ability to directly or indirectly optimize the ply thickness, ply orientation and stacking sequence for composite structures.
Free-size optimization handles the thickness of each ply in each element as a design variable and optimizes the structure by determining the optimal thickness distribution for each ply in the laminate.
For several reasons, every composite manufacturer has their own manufacturability standards for the laminated composites. These additional manufacturing constraints are to be included with free-size optimization to achieve an acceptable manufacturing solution. OptiStruct supports different manufacturability constraints that can be defined with free-size optimization. This tutorial helps explain the procedure used to define the manufacturing constraints in the free-size optimization of composite structures.
- Objective
- Minimize the Mass.
- Constraints
- Displacement of selected 6 nodes < 3 mm.
- Design Variables
- Thickness of each ply of each element in the design space.
Launch HyperMesh and Set the OptiStruct User Profile
Open the Model
Review the Model Setup
In this step you will use HyperLaminate to define, review, and edit ply lay-up information.
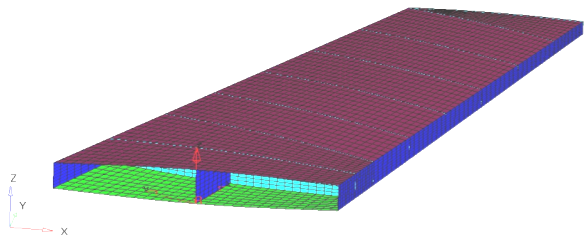
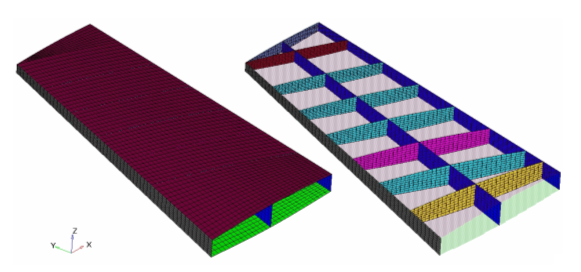
The model is already set up for the analysis. The model properties, loads, boundary conditions, and loadsteps are already defined. The model has 15 components out of which the TopSkin and BottomSkin components are defined with the composite property PCOMP. The rest of the components are defined with PSHELL property which references the material property, Aluminum.
Set Up the Optimization
Create Design Variable
- From the Analysis page, click the optimization panel.
- Click the free size panel.
- Select the create subpanel.
- In the desvar= field, enter Skins.
- Set type: to PCOMP(G).
- Using the props selector, select the TopSkin and BottomSkin properties.
- Clicks create.
Add a Minimum Dimension Manufacturing Constraints
- Select the parameters subpanel.
- Click desvars= and select Skins.
- Toggle minmemboff to mindim =, and enter 5.0.
- Click update.
Add Minimum Thickness Manufacturing Constraints
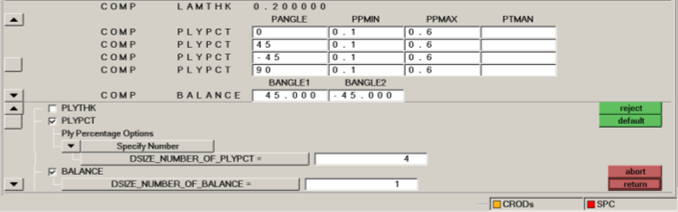
- Minimum laminate thickness of 0.2.
- A Minimum of 10% and a maximum of 60% thickness (of total laminate thickness) constraints defined for all the plies. This means that for each element, none of the plies will have thickness less than 10% or greater than 60% of the totals laminate thickness.
- The thickness of ply with ply angle of 45 degree to be same as the thickness of ply with ply angle of -45 degree.
Create Optimization Responses
- From the Analysis page, click optimization.
- Click Responses.
-
Create the mass response, which is defined for the total volume of the
model.
- In the responses= field, enter mass.
- Below response type, select mass.
- Set regional selection to total and no regionid.
- Click create.
-
Create the displacement response.
- Click return to go back to the Optimization panel.
Create Design Constraints
- Click the dconstraints panel.
- In the constraint= field, enter disp_constr.
- Click response = and select disp.
- Check the box next to upper bound, then enter 2.0.
- Using the loadsteps selector, select Subcase1 and Subcase2.
- Click create.
- Click return to go back to the Optimization panel.
Define the Objective Function
- Click the objective panel.
- Verify that min is selected.
- Click response and select mass.
- Click create.
- Click return twice to exit the Optimization panel.
Run the Optimization
View the Results
OptiStruct provides element thickness, ply thickness information for all iterations, and also writes out displacement and von Mises stress results for the linear static analysis. This section describes how to view the results in HyperView.
 to open the
to open the 
 to open the Iso panel.
to open the Iso panel. to activate the Component view.
to activate the Component view.
 (Isolate Shown) and click the
(Isolate Shown) and click the  to open the Exploded View panel.
to open the Exploded View panel.
