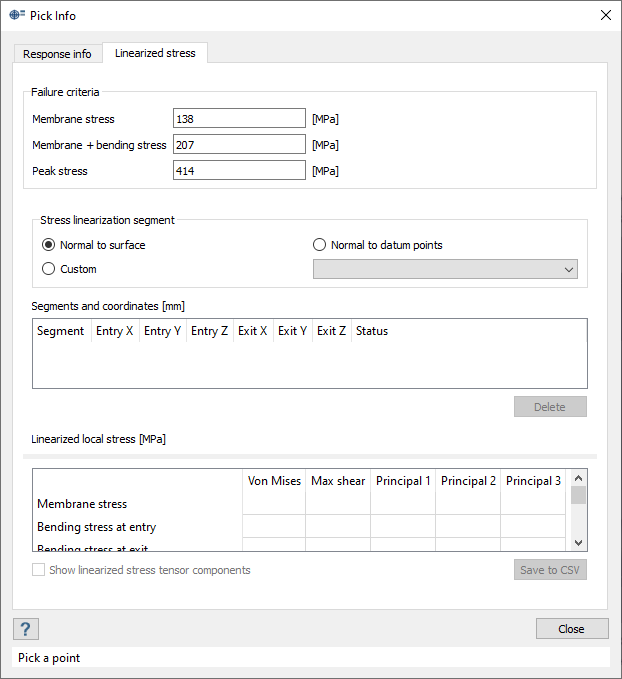
線形化応力の計算

該当する許容制限と比較するために、板厚方向の弾性応力場を、同等の膜応力、曲げ応力、およびピーク応力に分解します。

ProjectツリーでAnalysisワークベンチを開きます。
（Pick info）をクリックします。
ダイアログでLinearized stressタブを選択します。

図 1.
オプション: 膜応力、膜 + 曲げ応力およびピーク応力の疲労基準を入力し、作成されたセグメントの合格 / 不合格ステータスを確認します。デフォルト値は、材料の降伏応力を使用して計算されます。

膜応力 = 降伏応力の2/3

膜 + 曲げ応力 = 降伏応力

ピーク応力 = 2x 降伏応力

モデルに複数の材料が存在する場合、降伏応力が最も高い材料がデフォルトの許容値の計算に使用されます。

Stress linearization segmentで、以下のいずれかの方法でラインセグメントを定義します。

オプション	Steps
Normal to surface	Normal to surfaceラジオボタンを選択します。 SimSolidは、サーフェスに対して垂直で、パートを通過する光線を放ちます。
カスタム	Customラジオボタンを選択します。モデリングウィンドウで、パート上の開始ポイントと終了ポイントを選択します。開始ポイントと終了ポイントの座標がダイアログに入力されます。
Normal to datum points	Normal to datum pointsラジオボタンを選択します。ドロップダウンメニューでポイントセットを選択します。

定義されたラインセグメントごとに、線形化されたローカル応力がその場で評価され、ダイアログに転記されます。デフォルトでは、不変量がテーブルに表示されます。

Show linearized stress tensor componentsチェックボックスを選択して、不変量とともに応力テンソル成分を表示します。

ヒント: ラインのステータスには、疲労基準に基づいて合格または不合格が表示されます。疲労基準は不変量でのみ評価されます。
オプション: 線形化応力情報をCSVファイルとして保存します。
1. Save to CSVをクリックします。
2. ダイアログで、ファイル名を入力して、保存先を選択します。
3. Saveをクリックします。

計算方法

SimSolidによる線形化応力の計算方法

線形化応力では、該当する許容制限と比較するために、板厚方向の弾性応力場を、同等の膜応力、曲げ応力、およびピーク応力に分解します。

線形化応力は以下のように計算されます：

応力は、ラインに沿ったすべてのポイントでローカル座標系の補間によって抽出されます。ローカル座標系は、応力線形化セグメントの開始ポイントと終了ポイントを基準にしています。
ローカル座標系のX軸は、開始ポイントから終了ポイントまでのセグメントに沿っています。他の2つの軸は以下のように計算されます：
- ローカルx軸がグローバルy軸と平行でない場合：
  Z_local = X_local x Y_global
  
  Y_local = Z_local x X_local
- ローカルx軸がグローバルy軸と平行な場合：
  ローカルxが正のグローバルyに沿っている場合、ローカルy軸（Y_local）はグローバルxの負であり、その逆も同様です。
  
  Z_local = X_local x Y_local
上記の抽出された応力値から、数値積分を使用して、開始ポイントと終了ポイントでの平均膜応力力テンソル + 曲げ応力テンソルが計算されます。
$σ_{i}^{m} = \frac{1}{L} \int_{- L / 2}^{L / 2} σ_{i} d x$

$σ_{i S}^{b} = - \frac{6}{L^{2}} \int_{- \frac{L}{2}}^{\frac{L}{2}} σ_{i} x d x$

$σ_{i E}^{b} = - σ_{i S}^{b}$

$σ_{i}^{m}$ = 膜応力のi^th成分

$σ_{i}$ = 抽出された応力値のi^th成分

$σ_{i S}^{b}$ = 開始ポイントでの曲げ応力のi^th成分

$σ_{i E}^{b}$ = 終了ポイントでの曲げ応力のi^th成分

L = 応力線形化セグメントの長さ

x = セグメントに沿ったポイントの位置
ピーク応力と膜および曲げ応力も開始ポイントと終了ポイントで計算されます。
$σ_{i S}^{p} = σ_{i S} - (σ_{i}^{m} + σ_{i S}^{b})$

$σ_{i E}^{p} = σ_{i E} - (σ_{i}^{m} + σ_{i E}^{b})$

$σ_{i S}^{p}$ = 開始ポイントでのピーク応力のi^th成分

$σ_{i E}^{p}$ = 終了ポイントでのピーク応力のi^th成分
最後に、膜応力、膜 + 曲げ応力、およびピーク応力の不変量が計算されます。