SS-V：6030 単純支持された正方形薄板 - 周波数応答
テスト番号VD04単純支持された正方形板の周波数応答を表示します。
定義
単純支持された正方形薄板（10 x 10 x 0.05 m）が、次の関数のように時間変動する均一な圧力P=100 Paを受けます。(1)
ここで、
- 励振振動数。
動解析の解を近似するために16個のモードが使用され、すべてのモードで2%のモーダル減衰が仮定されます。
材料特性は以下の通りです：
- 特性
- 値
- 弾性係数
- 2.e+11 Pa
- ポアソン比
- 0.3
- 密度
- 8.e+3 kg/m3
注: このテストはテストVD01と似ていますが、周波数領域で解かれます。
結果
板は3Dソリッドボディとしてシミュレートされます。ヒンジ拘束を適用するために、板の中心面でスポットラインが作成されました（図 1）。
図 1.
励振振動数が板の最初の固有振動数に等しくなると、ピーク応答に達します。図 2 は、選択したポイント（座標 [m] X = 4.9469, Y = 0.05., Z = -4.9158）のY変位振幅に対する周波数掃引の結果を示しています。
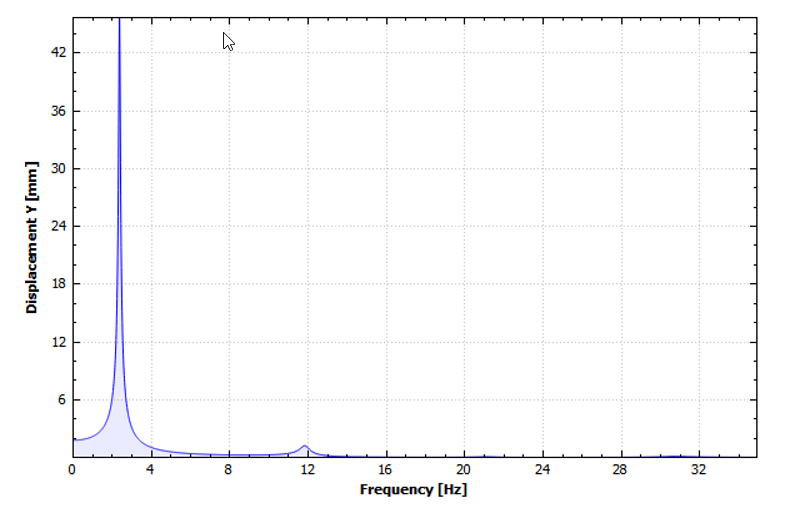
図 2.
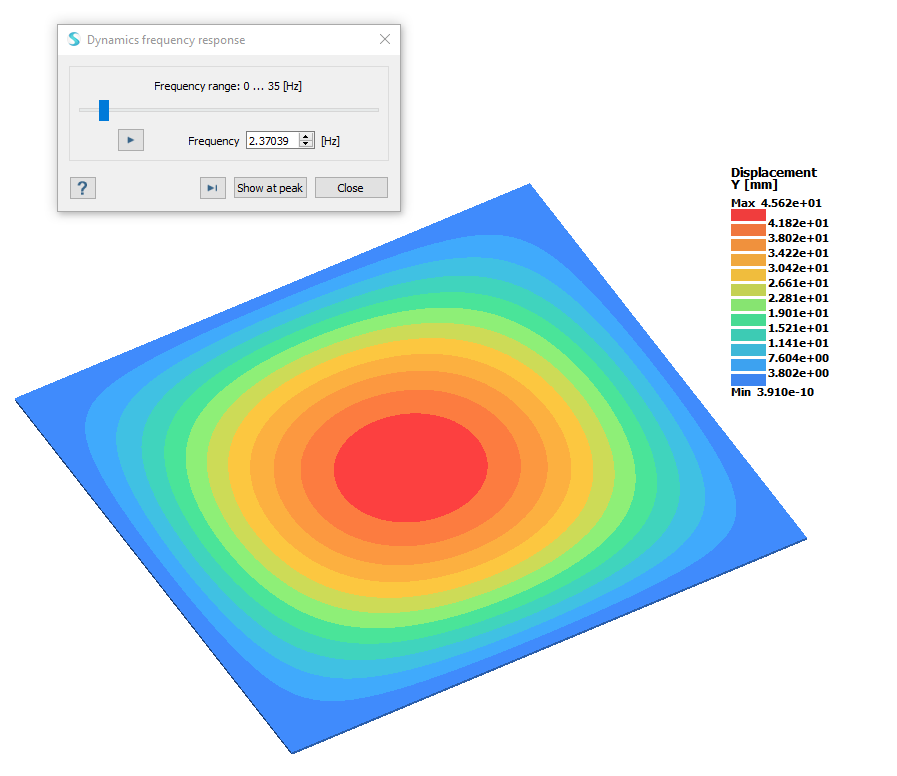
図 3.
次の表は、ピーク応答の比較を示しています。
| たわみY振幅、mm | 表面応力振幅、MPa | |
|---|---|---|
| 45.68 | 32.52 | SimSolid、3Dソリッドモデル |
| 45.42 | 35.08 | 基準、薄板モデル |
1
Test 13H from NAFEMS Publication R0016, “Selected Benchmarks for Forced Vibration” J. Maguire, D.J.Dawswell, L. Gould