Built-In Library of Methods

You can chain another method which leverage data extracted from JointLoad to calculate a margin of safety.

Box length=0.4*scale*(material scale*Diameter)

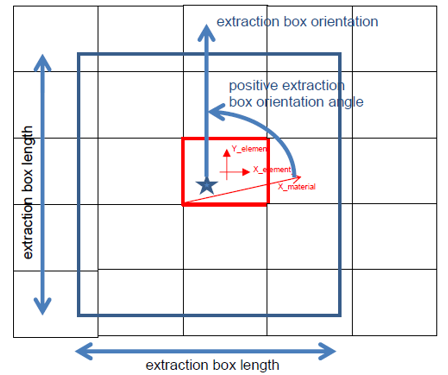
Figure 1.

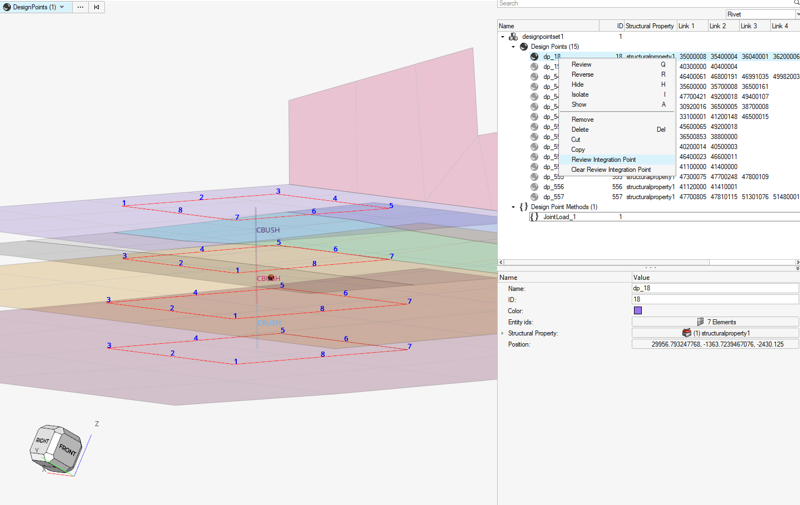
Figure 2. Review extraction areas per plate

The Panel_composite config comes with a set of various composite laminates first ply failure criteria. All of these failure criteria are bundled in a single certification method called “First_Ply_Failure”. This method internally invokes former ESACOMP engine.

Despite the method being available under the Panel_composite config, it evaluates failure criteria per element basis. As mentioned before, if the structural property assigned to a given designpoint refers to a user-defined property (PCOMP or PCOMPG), then all attributes required by the method are queried from this property. Otherwise, it will go directly per element’s property (supports PCOMP, PCOMPG, PCOMPP properties and MAT1, MAT8 cards).

All composite stresses are recalculated from shell element forces and moments based on the reference laminate property used. It then requires that result files contain shell element resultant forces and moments.

Math

Shell element resultant forces and moments (F/M/Q) are read from the result file and translated to the material orientation system based on the model. The moment sign conversion follows the notation used in [1]. Resultant forces and moments are translated to the geometrical mid-plane of the laminate. For ply-based models, local zone-laminates are automatically created. Strains and stresses are resolved at the three recovery planes of each layer using the Classical Lamination Theory. Out-of-plane shear stresses are determined based on [2] when needed. First ply failure-based analysis is performed for the selected design criteria and material combinations with single or multiple loadcases. For the required strength allowable, refer to the table below.

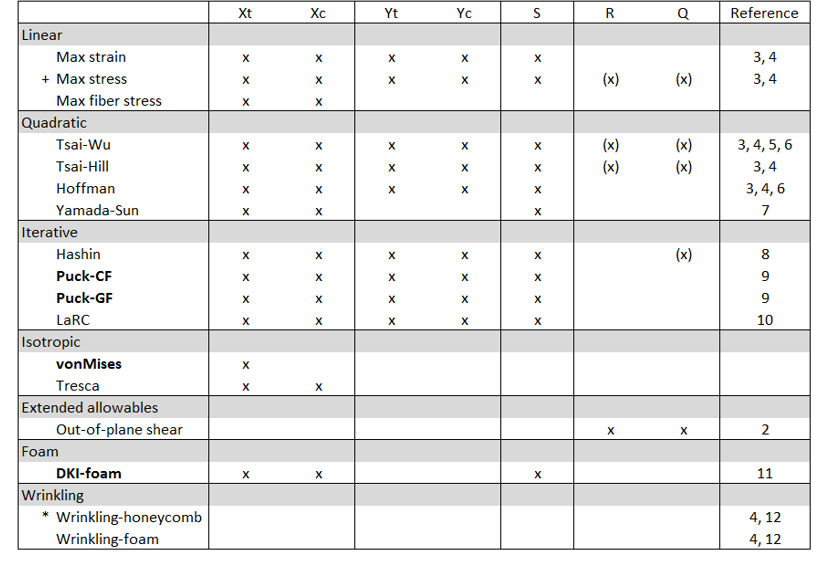
Figure 3. Required allowable per criteria

+ Max stress for isotropic material requires Xt, Xc and S and considers out-of-plane shear.

The bolded design criteria automatically considers out-of-plane shear stresses.

If R and Q (for MAT8) are defined, traditional in-plane criteria will also consider the out-of-plane shear.

Terminology

Reserve Factor is a measure of margin to the onset of failure. The effective load multiplied with the Reserve Factor gives the design margin. Thus, Reserve Factor values greater than one indicate a positive design margin and values less than one indicate a negative design margin. The values of Reserve Factors are always greater than zero. The term Factor of Safety is used with the Reserve Factor/Inverse Reserve Factor/Failure Index; this is determined as inv(Reserve Factor).

For linear criteria (max strain, max stress and max fiber stress), it is equal to the value of the failure function f.

Margin of Safety = Reserve Factor – 1.

Activate Failure Theories

Once the First_Ply_Failure method is added to a designpointset, you can edit it from the browser. First, you can select the result level (Element | Layer | Recovery plane), then the type of margin to evaluate.

The failure theories that are available are grouped in categories in the Entity Editor, as per the description in Figure 3. You will activate methods of interest by providing materials to use for failure evaluation (Figure 4). As listed in Figure 3, all failure theories require allowable to be set directly in the referred material entities. Whenever these allowables are meant to be available directly as a solver card (MAT1/MAT8 attributes), they will be queried from the material card. Extra allowables, not available from the solver deck, are automatically created as metadata attached to referenced material entity in HyperMesh. Metadata can be edited in each material Entity Editor. If a metadata already exists, it will not be overridden. Metadata is stored in the HyperMesh binary file along with the model.

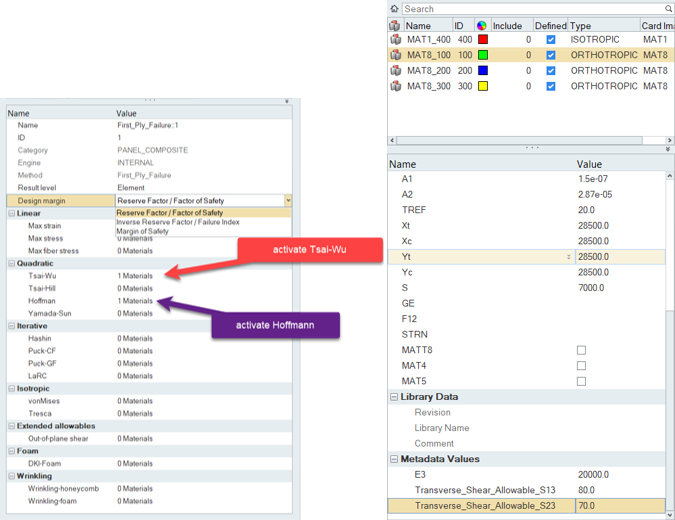
Figure 4. First ply failure selection & allowable as metadata

Example 1: Local Post-Processing

A corner supported uniformly pressure-loaded thick cross-ply laminated plate [13]. This tutorial highlights post-processing for four specific elements using two design criteria, namely Max strain and Out-of-plane shear. The latter requires additional strength allowable in the out-of-plane shear direction, which are introduced as HyperMesh metadata.

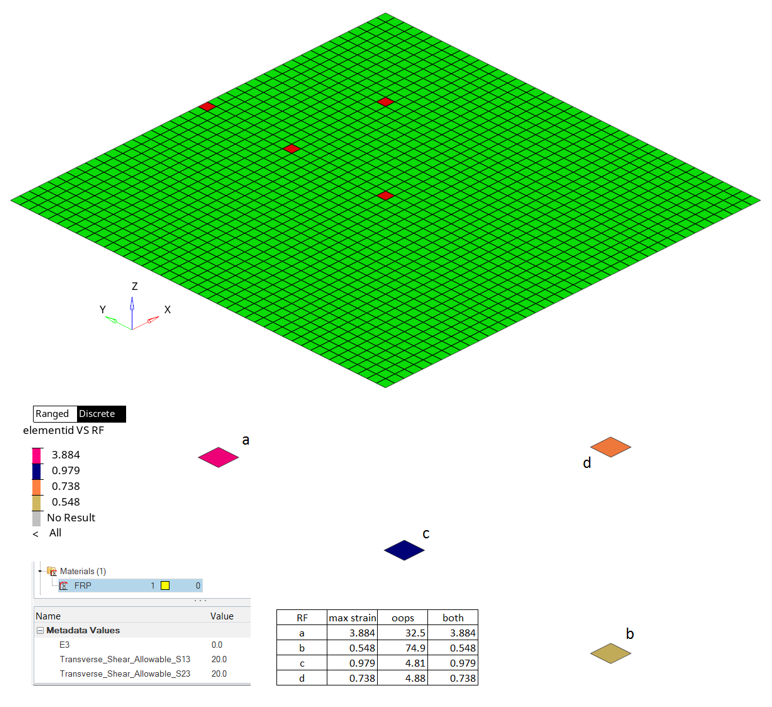
Figure 5.

Example 2: Global Post-Processing

Filament wound Composite Pressure Vessel (CPV) loaded with internal pressure. The CPV is wound from seven helical GFRP layer pairs and one circumferential CFRP layer pair. FPF results for the CPV are presented in the element level and layer level using Max strain criterion. For comparison, Yamada-Sun criterion-based results are presented in the element level. Finally, post-processing is performed only for the CFRP material using Max fiber stress criterion.

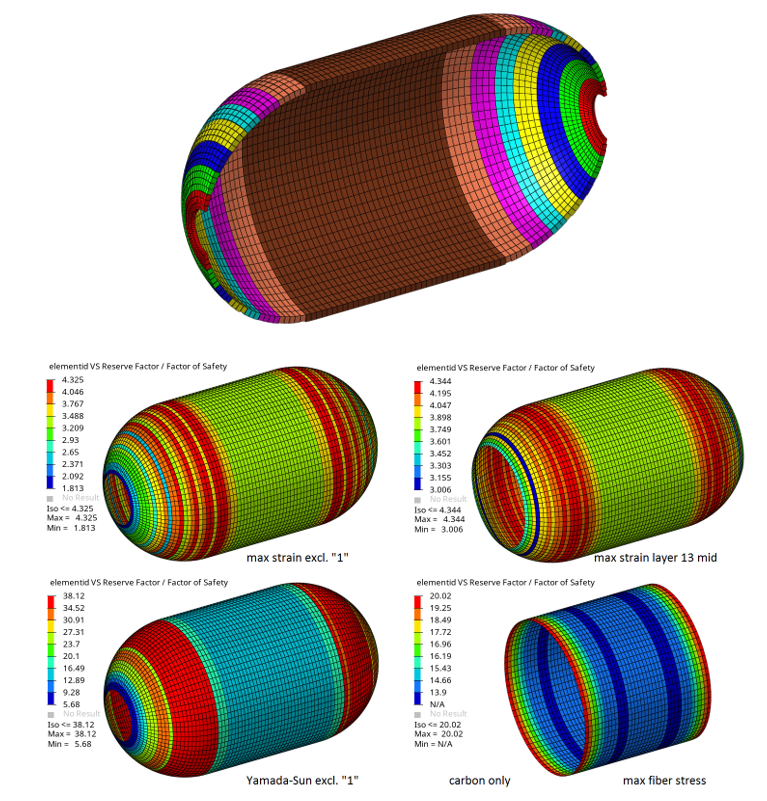
Figure 6.

First Ply Method References

The Panel_metallic configuration is shipped with a DLL method called Panel_FailureMode. It computes four possible failure modes for a metallic panel. The method requires shell element forces to be available in the result file. It assumes a valid panel with constant thickness and retrieves thickness information from its structural property. Panel thickness is used to recompute element stress XX, YY, XY. Similarly, the structural property’s material is used to extract tensile/compressive and shear allowable. The method evaluates Margin of Safety as MS= Allowable/Stress -1 for the three directions. For directions one and two (XX and YY), depending on the stress state, either tensile or compressive allowable is used. For shear (XY) absolute stress value is considered in the margin of safety formula.

A fourth failure mode is computed as shear buckling failure of curved panel. In the latter, the highest shear force seen by all elements in the design point is considered. Shear buckling is a ratio of stress with F_scrit = $$\pi$$²K_cE/(12*(1- $$v$$²)*(t/b)² where Kc=Rs+0.2*W²/(R*T).

Rs is available as structural property metadata Radius_shear_constant and the default is 5.35.

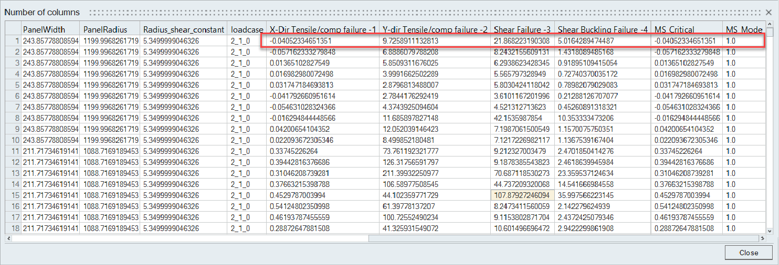
Figure 7. Panel Metallic Failure method

The Stinger Axial Stress is a simple method which calculates the Compressive/Tensile margin of safety as:

MS= [(Compressive Stress limit)*(section Area)/(Axial Force)] -1; (resp. Tensile Stress limit)

In the case of freebody sections, Axial Force is mapped to the freebody resultant Fx.