Composite Topology and Free-size Optimization
For composite structures, topology and free-size optimization are defined through the DTPL and DSIZE Bulk Data Entries, respectively.
Both are supported in the HyperMesh Optimization panel. Features available include: minimum member size control, symmetry, pattern grouping and pattern repetition.
Topology and free-size methods target a system level composite design where laminate family definition is the objective. Therefore, the PCOMP model should not reflect a detailed stacking of plies of the same orientation. For example, even though 10 layers of 0 degree graphite cloth might be separated in the stacking of the final structure, the modeling for a concept study using topology and free-size should group them together in one ply in the PCOMP, so that the optimal total thickness distribution of a 0 degree ply is optimized throughout the structure.
Problem Formulation

Figure 1. Composite Shell Element
The only difference between topology and free-size here is that the former targets a discrete final solution of 0 (or Ti) for ti, while free-size allows ti to vary freely between 0 and Ti. The discrete solution is achieved by penalizing intermediate thickness. Most general characteristics of regular shell topology and free-size optimization also apply to composite. It is recommended to become familiar with Free-size Optimization before proceeding. The major differences between topology optimization and free-size can be illustrated through a simple example.
Example: Cantilever Plate
The cantilever plate shown in Figure 2. A symmetric lay-up of (0, +45, -45, and 90) degree plies are used. The optimization problem is stated as:
Minimize Compliance
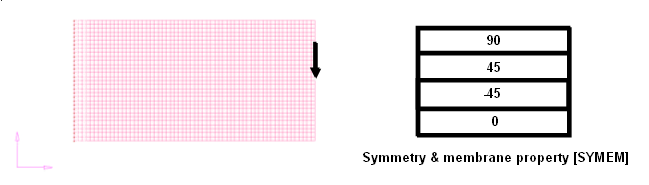
Figure 2. Composite Cantilever Plate
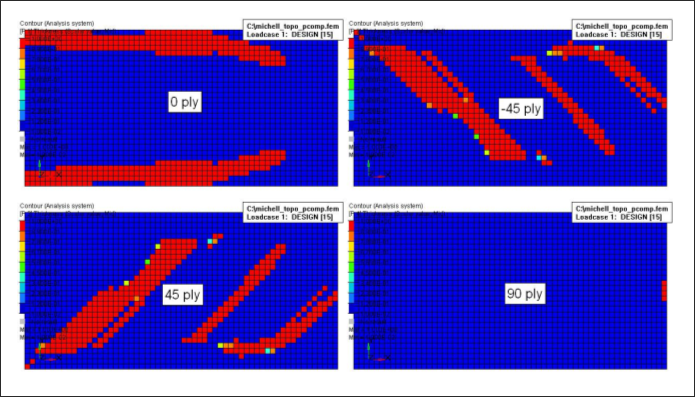
Figure 3. Topology Result - Thickness of Individual Plies

Figure 4. Topology Result - Total Thickness of the Laminate
It can be seen that a rather discrete thickness for each ply is obtained. While little overlapping of different orientations is shown in this result, it should be expected that overlapping of plies of different angles might be more pronounced when multiple load cases exist.
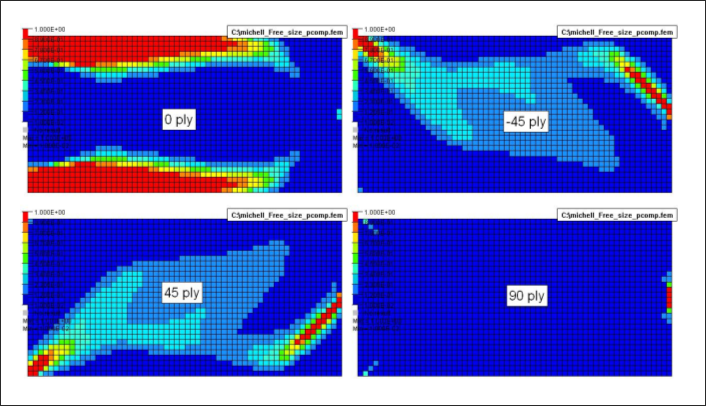
Figure 5. Free-size Result - Thickness of Individual Plies
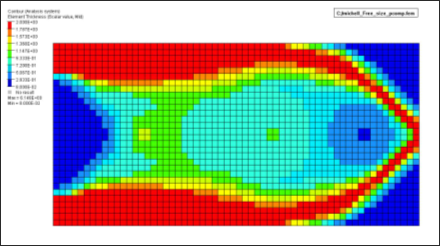
Figure 6. Free-size Result - Total Thickness of the Laminate

Figure 7. Compliance of Topology and Free-size Results
While ply angles are not variables for topology and free-size optimization, thickness optimization of plies indirectly leads to a discrete optimization of angles. The available angles in the PCOMP can be interpreted as discrete angle variables. Also, while free-size often creates variable thickness distribution without extensive cavity, it does not prevent cavity if the optimizer demands it. For this example, there is cavity in the free-size results in the 45 degree region, adjacent to the support, and in the upper and lower corners of the free end.
Topology and Free-size Design Characteristics
Most of the characteristics for general shell discussed in the free-size section also apply to composite structures.
| Composite Topology | Composite Free-size |
|---|---|
| Angle optimized indirectly. | Angle optimized indirectly. |
| Goal -
0/Ti discrete thickness of
individual plies Restricted freedom |
Goal - variable thickness of
individual plies "Free" under upper bound Ti |
| Results - Truss-like design concepts. | Variable thickness panel likely for in-plane loading, 0/1 thickness likely when bending is dominant. |
| Not useful compared to Free-size? | Always better design? |
| Manufacture - not a factor for composite unless pre-manufactured laminate is used. | Manufacture - naturally achieved with no additional cost. |
| Concentrated full thick members are stronger against out of plane buckling. | Spread thin shell could be prone to buckling. |
| Functionality may need holes for other non-structural components or for passing lines/pipes. | Cavity is controlled by optimality, and is usually not extensive under in-plane loading. |
Interpret Topology and Free-size Results
Interpretation of topology results is rather straight-forward. For free-size, the change in thickness of individual plies provides insight for ply dropping/adding zones.
The thickness of each ply in each individual zone can then be defined as a design variable in a detailed size optimization. At this stage, discrete variables can be used to reflect the discrete nature of ply thickness change. Overlapping all zones of individual plies can then help to generate PCOMP zones, where a ply traveling through different zones can be defined using PCOMPG.