LAW19 and LAW58 for Fabric
Radioss has two material laws for modeling fabrics LAW19 and LAW58. LAW19 is an elastic orthotropic material and must be used with /PROP/TYPE9. LAW58 is hyperelastic anisotropic fabric material and must be used with /PROP/TYPE16.
Coupling between warp and weft directions could be defined in this material law to reproduce physical interaction between fibers. Both material laws are often used for airbag modeling.
- Nonlinear function (fct_IDi) curve to define the warp, weft and shear behavior
- Young's modulus, soften coefficient B, straightening
strain Si and fiber bending modulus reduction factor
Flexi
In warp and weft direction:
For in-plane shear in initial state, use . Once α (angle between wrap and weft) reaches (shear lock angle), then use GT to describe the strengthening.
if
if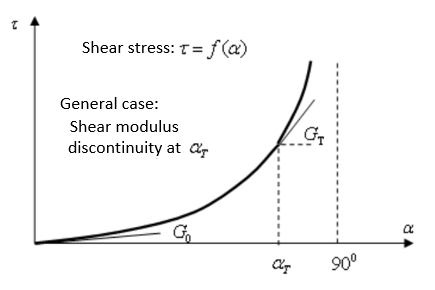
Figure 1.
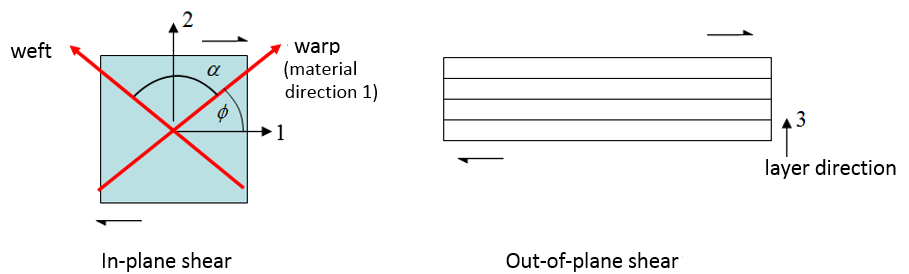
Figure 2.
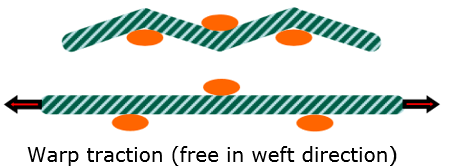
Figure 3.
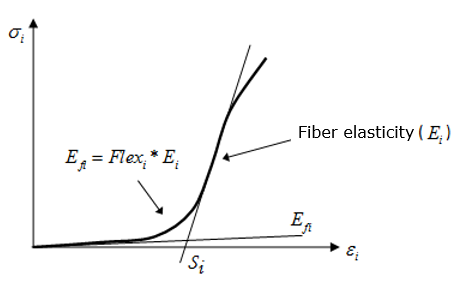
Figure 4.