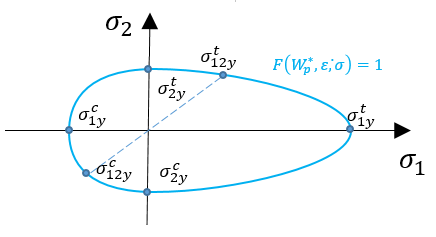
LAW25 (Tsai-WU and CRASURV)
LAW25 is the most commonly used composite material in Radioss. It can be used with shell and solid elements. The two formulations available in LAW25 are the Tsai-Wu and CRASURV formulations.
Elastic Phase
Tsai-Wu Yield Criteria for Iform=0 and =1
- Iform=0: Tsai-Wu
- Iform=1: CRASURV
- Tensile/compression tests
Longitudinal tensile/compression tests (in direction 1 which is fiber direction):

- Iform = 0: Tsai-Wu
- Iform = 1: CRASURV
- Here,
-
In tension:
In compression:
Here
Transverse tensile/compression tests (in direction 2)
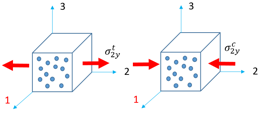
- Iform = 0: Tsai-Wu
- Iform = 1: CRASURV
- Here,
-
In tension:
In compression:
Here
- Shear tests
Shear in plane 1-2
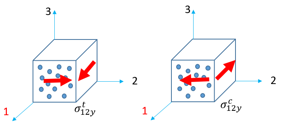
- Iform = 0: Tsai-Wu
- Iform = 1: CRASURV
- and can result from the sample tests:
-
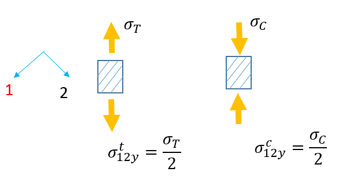
- Here,
- Interaction coefficients
- Iform = 0: Tsai-Wu
- Iform = 1: CRASURV
- The default reduction factor, , is typically used.
- Here,
- Iform = 0: Tsai-Wu
- Iform = 1: CRASURV
- With
- Here
- Material in elastic phase, if
- Material in nonlinear phase, if
-

- The yield stress limit is in range of 1 and
- Material in elastic phase, if
In LAW25 (Tsai-Wu and CRASURV) damage is a function of the total strain and the maximum damage factor.
- If the total strain is between , the material begins to soften, but this damage is reversible. Once , then the damage is irreversible and if , then stress in material is reduced to 0.
- Damage could be in elastic phase or in plastic phase. It depends on which phase and are defined in.
- Element deletion is controlled by Ioff. Select a different Ioff option to control the criteria of element deletion. For additional information, refer to Ioff in LAW25 in the Reference Guide.