/NONLOCAL/MAT
Block Format Keyword Non-local regularization for elasto-plastic failure criteria (as in, dependent to plastic strain) and shells thickness variation.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /NONLOCAL/MAT/mat_ID/unit_ID | |||||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit identifier. (Integer, maximum 10 digits) |
|
| Non-local internal
length. (Real) |
||
| Mesh convergence element length
target. (Real) |
Comments
- The non-local regularization is used to get mesh independent results
(size, orientation) in case of instabilities such as failure and/or
thickness variation (for shells). The mesh independent results implies a
mesh convergence for mesh sizes
less than or equal to the maximum value set
by you,
. This maximum mesh size
is then the highest mesh size used for which
results are mesh convergent. The non-local formulation is compatible with elasto-plastic material laws only. When activated, the computation of the attached failure criteria based on plastic strain and/or the shell thickness variation depends on a regularized nodal "non-local" plastic strain calculated on the entire mesh. The non-local plastic strain at nodes denoted is computed accounting for its own gradient and its local counterpart is computed at the Gauss points following the set of equations:
(1) The parameters and are automatically set. You have to set the parameter (or , Comment 2) which defines a non-local "internal length" corresponding to a radius of influence in the non-local variable computation. This defines the size of the non-local regularization band (Figure 1).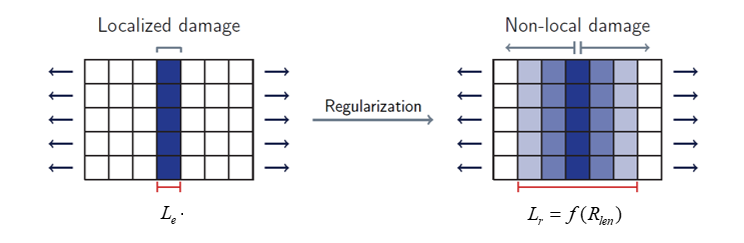
Figure 1. Non-local regularization principle illustrationThe failure criterion damage variable is then computed using the non-local plastic strain.(2) Where, is the plastic strain at failure depending on the failure criterion formulation.
- To set the non-local
length parameter
, you can select:
- Directly input the value of in the input card, if a direct control on this parameter is wanted. In this case, the parameter must be ignored.
- Input the maximum mesh size
for which results are mesh
convergent. The non-local regularization will then be effective for
all mesh sizes
such as
. In this case, an automatic set of
is realized according to the value
of
, and the input value of
is ignored.
For instance, if you want to get converged and mesh-independent results for a mesh size of 5mm, mm. In this case, the results will be converged, mesh-size and mesh orientation independent for mm.
- When the non-local regularization is used for shell elements, an
additional regularization is made on the thickness variation computation
avoiding an additional localization issue. In the common local case (Figure 2), the compatibility of thickness
between shell elements is not ensured, due to the lack of kinematic
equations in the z-direction, and the thickness variation is locally
computed at Gauss points. By introducing the non-local plastic strain in the
"in-thickness" strain increment, the compatibility is restored (Figure 3).
(3) Where, is the non-local plastic multiplier.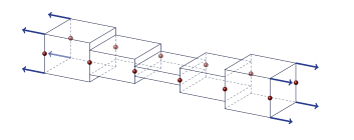
Figure 2. Transverse strain incompatibility (local)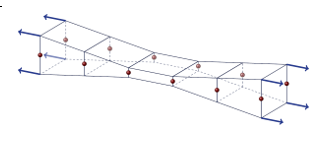
Figure 3. Transverse strain compatibility (non-local)Note: This last point implies that the identified parameters can be used on solid and shells, as results will be identical within the same range of stress triaxiality . - List of compatible material laws for shells thickness variation
regularization:
- /MAT/LAW2 (PLAS_JOHNS)
- /MAT/LAW22 (DAMA)
- /MAT/LAW27 (PLAS_BRIT)
- /MAT/LAW32 (HILL)
- /MAT/LAW36 (PLAS_TAB)
- /MAT/LAW43 (HILL_TAB)
- /MAT/LAW44 (COWPER)
- /MAT/LAW48 (ZHAO)
- /MAT/LAW57 (BARLAT3)
- /MAT/LAW60 (PLAS_T3)
- /MAT/LAW63 (HANSEL)
- /MAT/LAW64 (UGINE_ALZ)
- /MAT/LAW72 (HILL_MMC)
- /MAT/LAW76 (SAMP)
- /MAT/LAW78
- /MAT/LAW87 (BARLAT2000)
- /MAT/LAW93 (ORTH_HILL) (CONVERSE)
- /MAT/LAW104 (JOHNS_VOCE_DRUCKER)
- /MAT/LAW109
- /MAT/LAW110 (VEGTER)
- List of elasto-plastic failure model and coupled damage model
compatible with non-local regularization:
- MMC damage model in /MAT/LAW72
- Damage model in /MAT/LAW76
- /FAIL/BIQUAD
- /FAIL/COCKROFT
- /FAIL/EMC
- /FAIL/HC_DSSE (for shells)
- /FAIL/JOHNSON
- /FAIL/ORTHBIQUAD
- /FAIL/RTCL
- /FAIL/SPALLING
- /FAIL/TAB1
- /FAIL/USERi
- /FAIL/WIERZBICKI
- /FAIL/WILKINS
- List of material laws with non-local regularized temperature computation:
- /MAT/LAW104 (JOHNS_VOCE_DRUCKER)
- /MAT/LAW109