/MAT/LAW44 (COWPER)
Block Format Keyword The Cowper-Symonds law models an elasto-plastic material. The basic principle is the same as the standard Johnson-Cook model; the only difference between the two laws lies in the expression for strain rate effect on flow stress.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW44/mat_ID/unit_ID or /MAT/COWPER/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | |||||||||
| a | b | n | Chard | ||||||
| c | p | ICC | Fsmooth | Fcut | VP | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_IDy | Fscaley | ||||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| mat_title | Material
title. (Character, maximum 100 characters) |
|
| Initial
density. (Real) |
||
| E | Young's
modulus. (Real) |
|
| Poisson's
ratio. (Real) |
||
| a | Plasticity yield
stress. (Real) |
|
| b | Plasticity
hardening parameter. (Real) |
|
| n | Plasticity
hardening exponent. Default = 1.0 (Real) |
|
| Chard | Plasticity
Iso-kinematic hardening factor.
Default = 0.0 (Real) |
|
| Plasticity maximum
stress. Default = 1020 (Real) |
||
| c | Strain rate coefficient.
(Real) |
|
| p | Strain rate
exponent. Default = 1.0 (Real) |
|
| ICC | Strain rate
computation flag. 6
(Integer) |
|
| Fsmooth | Smooth strain rate
option flag.
(Integer) |
|
| Fcut | Cutoff frequency
for strain rate filtering. Default = 1030 (Real) |
|
| VP | Formulation for
rate effects.
(Integer) |
|
| Failure plastic
strain. Default = 1020 (Real) |
||
| Tensile failure
strain 1. Default = 1020 (Real) |
||
| Tensile failure
strain 2. Default = 2x1020 (Real) |
||
| fct_IDy | Yield stress
function identifier. (Integer) |
|
| Fscaley | Scale factor for
ordinate (stress) in
fct_IDy Default = 1.0 (Real) |
Example (Metal)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
g mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/COWPER/1/1
metal
# RHO_I
.0078
# E nu
20500 .3
# a b n C_hard SIGMA_max0
50 100 .5 1 90
# c p ICC Fsmooth F_cut
100 5 1 0 0
# EPS_max EPS_t1 EPS_t2
0 0 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- The yield stress can be defined by the
three stress coefficients (a,
, and
), a function
fct_IDy, or a
combination of both. The stress is then scaled by the Cowper-Symonds strain
rate coefficient.
- If fct_IDy is
defined (> 0), a=0 and
VP=1:
(1) - If fct_IDy is
defined (> 0) and a >
0:
(2) - If fct_IDy is not
defined (= 0):
(3)
Where,- Plastic strain.
- Plastic strain rate for VP =1.
- If fct_IDy is
defined (> 0), a=0 and
VP=1:
- The law is compatible with truss, beam, shell, and solid elements.
- Yield stress should be strictly positive.
- The hardening exponent
n must be less than 1.
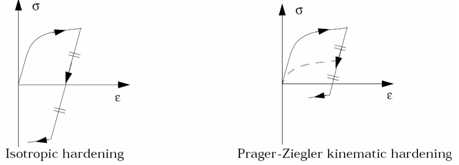
Figure 1. - The strain rate filtering
is used to smooth strain rates, with the following:
- If VP = 1, the strain-rate filtering is set by default and the cutoff frequency is automatically computed by Radioss according to time step value. Fcut and Fsmooth are ignored.
- If VP = 2 or
3, and:
- Fsmooth = 0 + Fcut = 0.0, the strain-rate filtering is turned off;
- Fsmooth = 1 + Fcut = 0.0, the strain-rate filtering uses a cutoff frequency which is automatically computed by Radioss according to time step value (as for VP = 1);
- Fcut ≠ 0, Fsmooth is automatically set to 1 and the strain-rate filtering uses the cutoff frequency provided by the user.
- ICC is a flag of the strain rate effect on material maximum stress
:
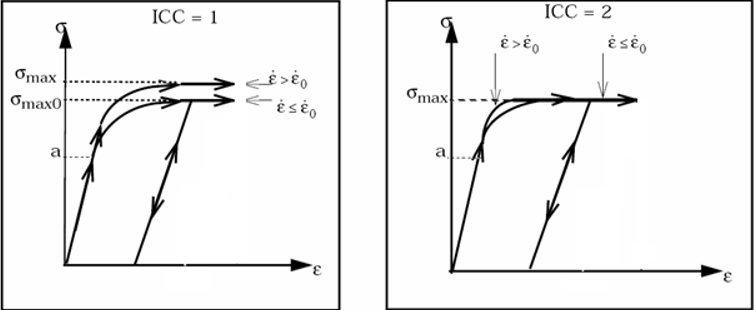
Figure 2. - When
reaches
in one integration point, then based on the element
type:
- Truss and Beam elements: The element is deleted
- Shell elements: The corresponding shell element is deleted
- Solid elements: The deviatoric stress of the corresponding integral point is permanently set to 0; however, the solid element is not deleted
- If
(
is the largest principal strain), the stress is reduced
as:
(4) - If , the stress is reduced to 0 (but the element is not deleted).