/MAT/LAW93 (ORTH_HILL) or (CONVERSE)
Block Format Keyword This law describes the orthotropic elastic behavior material with Hill plasticity and is applicable to shell and solid elements (/BRICK, /TETRA4 and /TETRA10).
It could be used with property set /PROP/TYPE11, /PROP/TYPE17, /PROP/TYPE51, /PROP/PCOMPP for shell and /PROP/TYPE6 for solid.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW93/mat_ID/unit_ID or /MAT/ORTH_HILL/mat_ID/unit_ID or /MAT/CONVERSE/mat_ID/unit_ID/ | |||||||||
| mat_title | |||||||||
| E11 | E22 | E33 | G12 | ||||||
| G13 | G23 | ||||||||
| Nrate | VP | Fcut | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_IDi | Fscalei | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| QR1 | CR1 | QR2 | CR2 | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| R11 | R22 | R12 | |||||||
| R33 | R13 | R23 | |||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| mat_title | Material title. (Character, maximum 100 characters) |
|
| Initial density. (Real) |
||
| E11 | Young’s modulus in direction
11. (Real) |
|
| E22 | Young’s modulus in direction
22. (Real) |
|
| E33 | Young’s modulus in direction
33. (Real) |
|
| G12 | Shear modulus in direction
12. (Real) |
|
| G13 | Shear modulus in direction 13.
(Real) |
|
| G23 | Shear modulus in direction 23.
(Real) |
|
| Poisson's ratio 12. (Real) |
||
| Poisson's ratio 13. (Real) |
||
| Poisson's ratio 23 (Real) |
||
| Nrate | Number of yield function. | |
| VP | Strain rate choice flag.
(Integer) |
|
| Fcut | Cutoff frequency for strain rate
filtering. Default = 1.0 x 104 (Real) |
|
| fct_IDi | Plasticity curves ith function
identifier (i=1,
Nrate). (Integer) |
|
| Fscalei | Scale factor for ith function (i=1,
Nrate). Default = 1.0 (Real) |
|
| Strain rate for ith function (i=1,
Nrate). (Real) |
||
| Initial yield stress. Default = 1E30 (Real) |
||
| QR1 | Parameter of hardening. Default = 0.0 (Real) |
|
| CR1 | Parameter of hardening. Default = 0.0 (Real) |
|
| QR2 | Parameter of hardening. Default = 0.0 (Real) |
|
| CR2 | Parameter of hardening. Default = 0.0 (Real) |
|
| R11 | Yield stress ratio in direction 11. Default = 1.0 (Real) |
|
| R22 | Yield stress ratio in direction 22. Default = 1.0 (Real) |
|
| R33 | Yield stress ratio in direction 33. Default = 1.0 (Real) |
|
| R12 | Yield stress ratio in direction 12. Default = 1.0 (Real) |
|
| R13 | Yield stress ratio in direction 13. Default = 1.0 (Real) |
|
| R23 | Yield stress ratio in direction 23. Default = 1.0 (Real) |
Example (Curve Input)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW93/1/1
plastic
# RHO_I
2.730E-09
# E11 E22 E33 G12 Nu12
225654 195400 178526 75187.97 0.30
# G13 G23 Nu13 Nu23
75187.97 75187.97 0.28 0.32
# Nrate VP Fcut
2 1 0.0
# Ifunct Yscale Epsdot
5 1.0 0.01
5 1.5 100.0
# SigY QR1 CR1 QR2 CR2
0 0 0 0.0 0.0
# R11 R22 R12
1.0 1.05626 0.96425
# R33 R13 R23
0.9337 1.0 1.0
/FUNCT/5
plastic
# X Y
0 165.6362749
0.002 173.8123558
0.005 180.2967164
0.01 186.5926709
0.02 193.8182168
0.05 204.4407991
0.07 208.5903797
0.1 213.1182051
0.12 215.4817557
0.15 218.4183864
0.17 220.0863912
0.2 222.2743041
0.22 223.5689486
0.25 225.3186882
0.27 226.3794409
0.3 227.840544
0.32 228.7406278
0.35 229.996802
0.37 230.7795124
0.4 231.8824363
0.5 235.0704031
0.6 237.7095003
0.7 239.9650034
0.8 241.9367878
0.9 243.689935
1 245.2692715
1.5 251.4456403
2 255.9237789
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- The yield stress is compared to an equivalent
stress in the orthotropic frame. For solid
elements, this equivalent stress is defined
as:
(1) Where,- Normal directions
- Shear directions
- Yield stress in direction
- Global flow stress that can either be defined with a sum of Voce hardening, or can be tabulated (see below).
- The
yield function
will compare the Hill’s equivalent stress
to the flow stress
as:
(3) The two different ways to define the flow stress are: parameter input or curve input- For parameter input, the flow stress is
defined with an initial yield stress and a double Voce hardening as:
(4) With .
- For curve input, the parameters input
values will be ignored. The yield can be defined with using stress versus plastic strain curve taking in account the strain rate effect. When the stress versus strain curves are defined, this is the default method for defining the hardening.
- If , the yield is interpolated between and .
- If function, is used.
- Above
, yield is extrapolated.
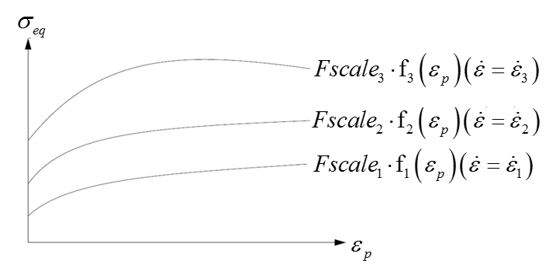
Figure 1.
- For parameter input, the flow stress is
defined with an initial yield stress and a double Voce hardening as:
- For
tabulated flow stress, the strain rate
computation depends on the value of the flag
VP.
- If VP= 1, the plastic strain rate is used
- If VP= 2, the total strain rate is used
- If VP= 3, the total strain rate is used
In all cases the strain-rate computation includes a filtering. The cutoff frequency is automatically set for VP = 1. However, for VP = 1 or 3, you can input a cutoff frequency Fcut; otherwise, a default value will be set.