RD-E: 4801 Solid Spotweld Validation
Introduces how to model a solid element spotweld using /MAT/LAW83 + /FAIL/SNCONNECT and validate results using experiment data.

Figure 1.
- Maximum stress and force
- Damage initiation displacement and failure displacement
Options and Keywords Used
- Solid spotweld material (/MAT/LAW83)
- Spotweld failure model (/FAIL/SNCONNECT)
- Solid spotweld property (/PROP/TYPE43 (CONNECT))
- Sheet metal material (/MAT/LAW1 (ELAST), /MAT/LAW2 (PLAS_JOHNS))
- Self-impacting contact (/INTER/TYPE7)
- Rigid body (/RBODY)
Input Files
Refer to Access the Model Files to download the required model file(s).
The model files used in this example are available in:
/radioss/example/48_solid_spotweld
Model Description
The spotweld is represented by one solid element connected the upper and lower sheets using a tied contact.
- Shear test (angle of load and sheet is 0°, below also named with 0° test)
- Normal test (90° test)
- Shear and normal combined tests (30° and 90° tests)
- Peel test
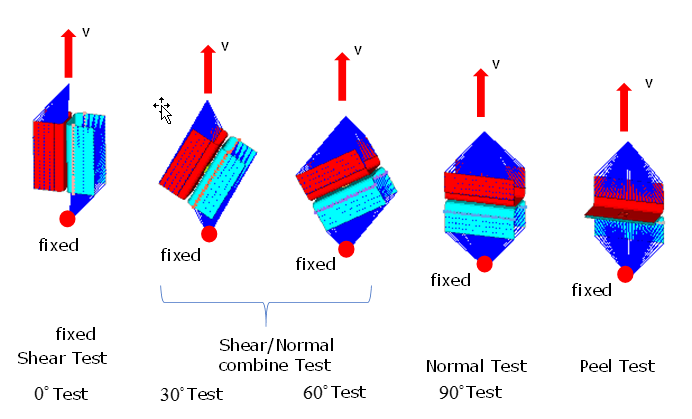
Figure 2.
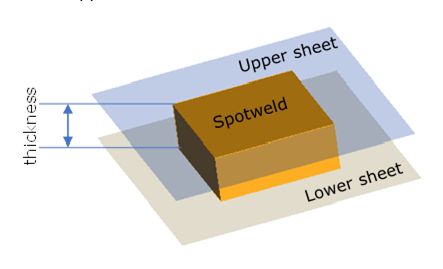
Figure 3. Problem Description
Units: mm, ms, Kg, kN, GPa
- Material Properties
- Initial density
- 7.85e-6 [Kg/mm3]
- Young's modulus
- 210 [GPa]
- Poisson ratio
- 0.3
- Yield stress
- 0.370 [GPa]
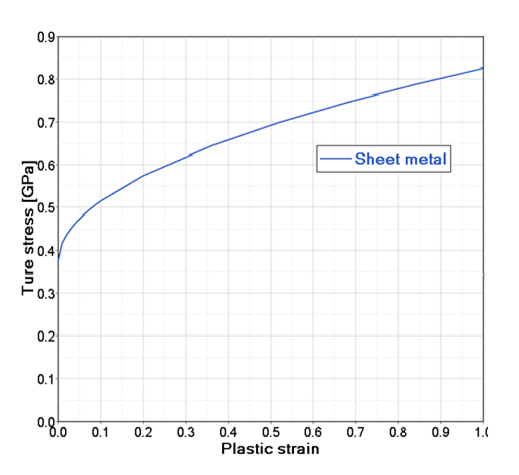
Figure 4. Sheet Metal Stress Strain Curve
Simulation Iterations
The spotweld is modeled using the connection material /MAT/LAW83 and connection failure /FAIL/SNCONNECT.
- Yield curve, fct_ID1
- Young's modulus
- Maximum stress in normal and shear direction with
- Maximum stress for loads that combine normal and shear loading
- Maximum stress in moment (peel test)
- and in normal and shear direction with (fct_ID0S), (fct_IDFS), (fct_ID0N), and (fct_IDFN)
- and in combined loading direction with
- and in moment (peel test) with
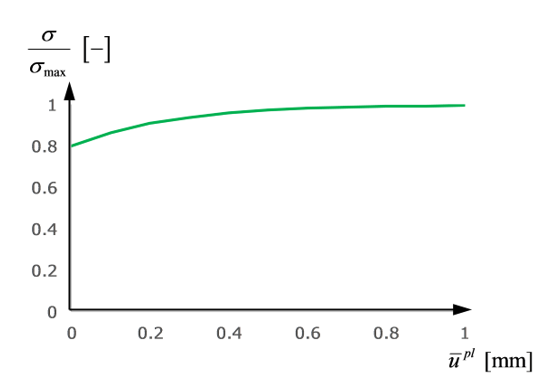
Figure 5. Normalized Yield Curve
The Young’s modulus in LAW83 could also take Young’s modulus from true stress versus displacement curve of 0° test.
The maximum stress in the normal direction and in tangent direction is extracted from the 90° test and 0° shear test and input as in LAW83.
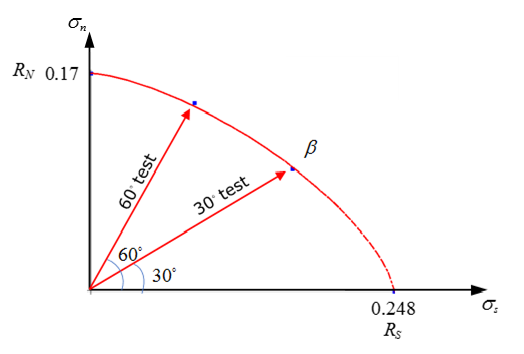
Figure 6. Yield Surface Fit Results for Combined Load Directions
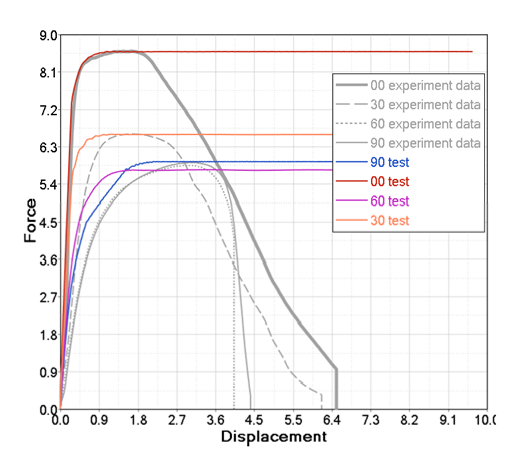
Figure 7. Simulation versus Test Results
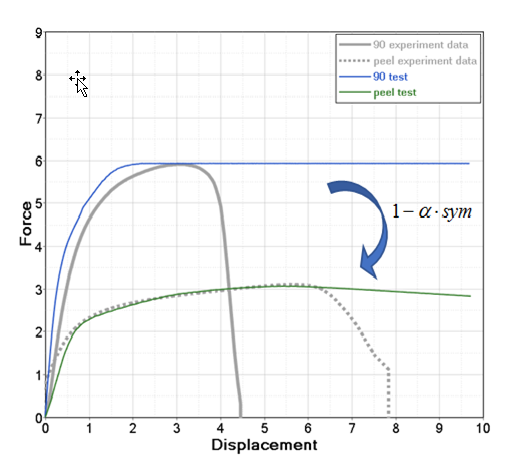
Figure 8. Simulation and Experimental Results for 90° and Peel Loads
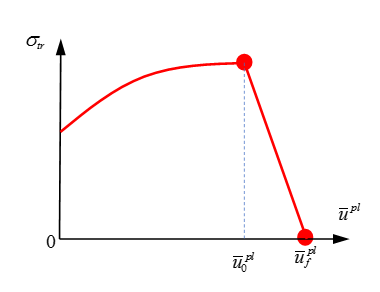
Figure 9. Stress versus Displacement Plot
- Spotweld failure in 90° (normal) and 0° (shear) testInput the displacement where damage begins and displacement at failure from the 90° test into functions ( (fct_ID0N) and ( (fct_IDFN) and from test into functions ( (fct_ID0S) and (fct_IDFS). Since there is no rate effect data, the curves will be constant.
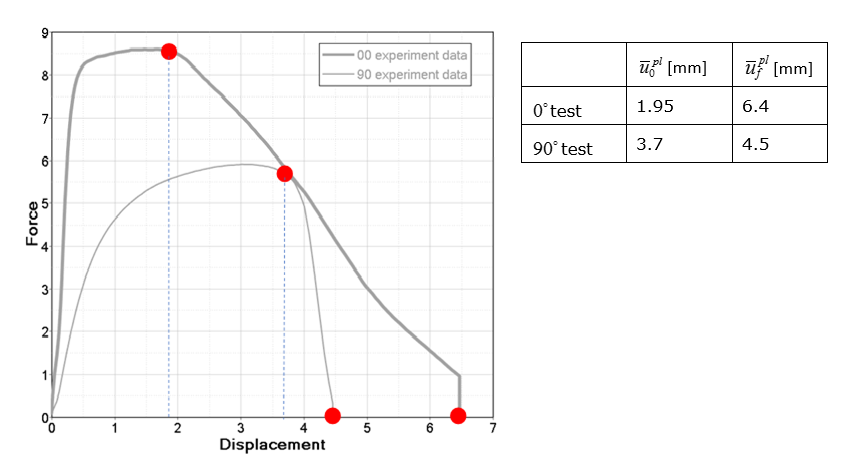
Figure 10. Beginnining and Failure Damage DisplacementsUsing these values in a simulation, the beginning damage displacement and failure displacement match very well to the 0° test results. However, the simulation does not match very well to the 90° test. This is due to the deformation of upper and lower sheet metal. In the 0° test, the sheet metal barely deforms.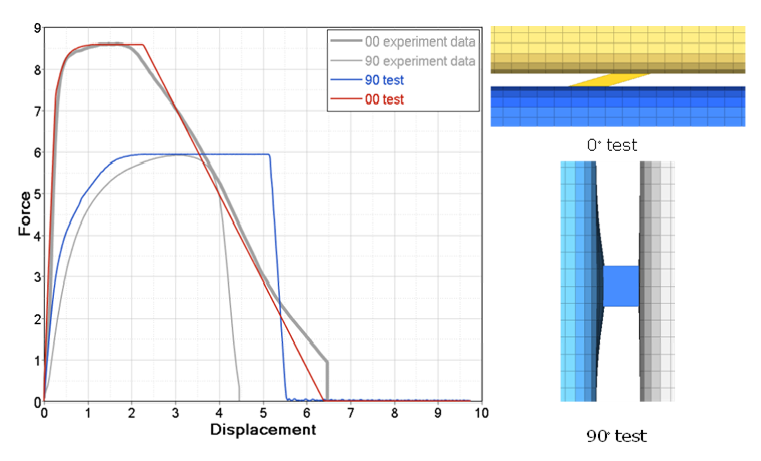
Figure 11. Simulation with Damage and Experimental Results. 0° and 90° testsUsing the displacement of the sheet metal from the simulation results, the sheet metal displacement is subtracted from the and of the 90° test. After doing this, the force displacement curves in the simulation match the test.
Figure 12. Improved Failure Results - Spotweld Failure in Combined TestsThe beginning and failure damage in the 30° and 60° tests (combined normal and shear loading) can be defined using the parameters in the following equations, which do not consider which are for peel test.
(4) (5) Taking and from experiment data: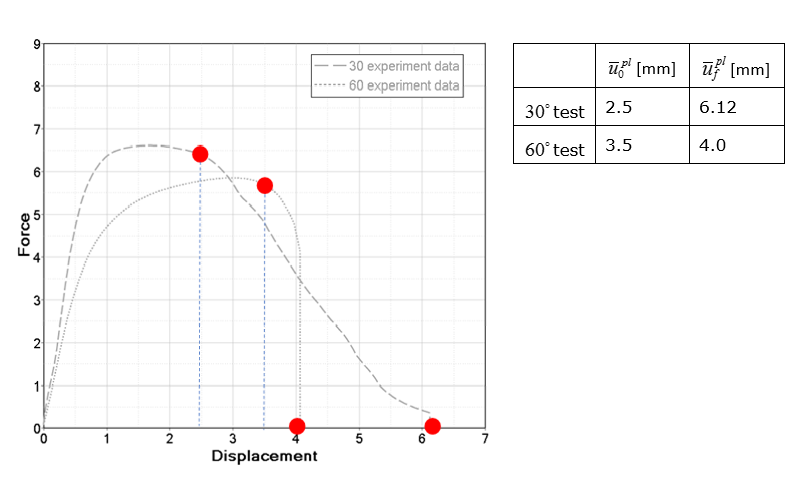
Figure 13. Test Results - 30° and 60°Using the results from the 30° and 60° tests, the and values are calculated using an equation fitting routine.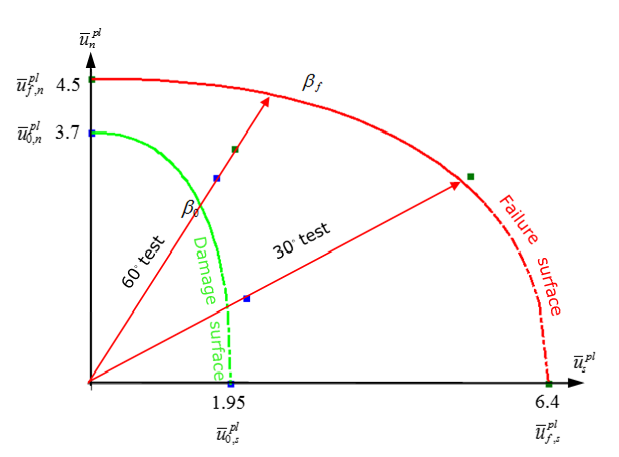
Figure 14. Damage and Failure Surface Fit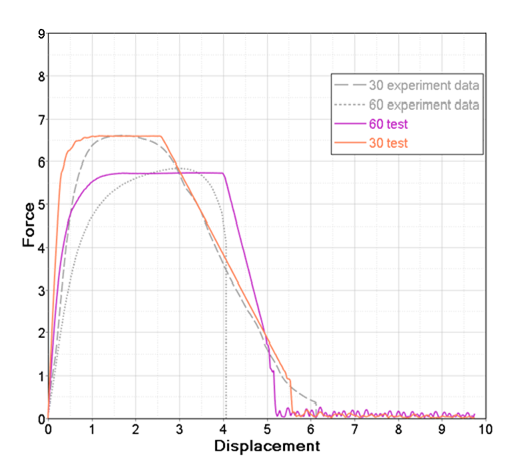
Figure 15. Results Initial Beta Parameter FittingUsing the calculated fitted parameters , the simulation shows that the start of the damage does not match the experimental data. Similar to the 90° test, the deformation of sheet metal needs to be excluded from the damage displacements. The sheet metal displacement from the simulation is subtracted from the damage displacement and new parameters and are calculated using the fitting algorithm.
Figure 16. Damage and Failure Surface Fit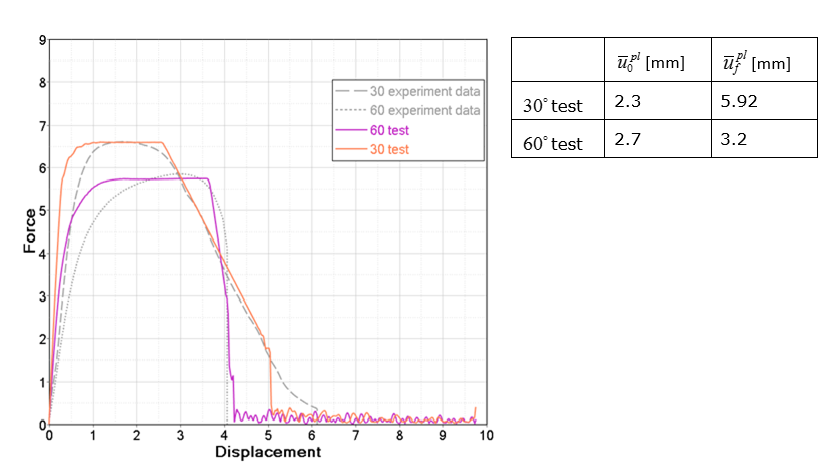
Figure 17. Validation - 30° and 60° TestsUsing the updated parameters, the beginning of the damage better matches the experiment data.
- Spotweld Failure in Peel Test
To correctly simulate the moment loads that occur in the peel test, the scale factor parameters must be calculated.
If the shear terms are ignored, the beginning and failure damage is represented as:(6) (7) The and terms scale the normal term in the equation. As done before for LAW83, the terms can be determined using the simulation and optimization or trial and error to match the peel test results. Starting with and the knowledge that increasing these terms decreases the and values, you determine that the parameters (peel test 2) result in and values that match the experimental peel test data.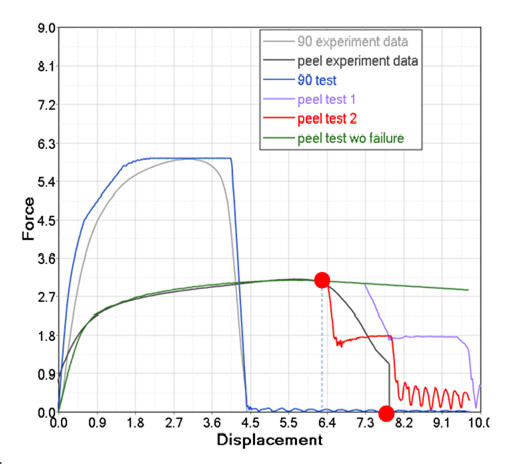
Figure 18. Validation - Peel Test
Results
With a minimum of 4 different experimental tests, input data for /MAT/LAW83 + /FAIL/SNCONNECT can be validated for use with solid brick element spotwelds.
Using a KS2 test specimen, a 0° test, 90° test, peel test and at least one combined loading (30, 45 or 60 degree) test is needed. Since there can be variations in the test data, it is better to have multiple test results for each test.
If upper and lower sheets deformed during the test, the simulations results can be used to modify the damage displacements during the validation of the spotweld failure displacement in /FAIL/SNCONNECT.