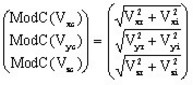Modulus functions: ModV, ModC and Mod
Before starting
The modulus functions, i.e. the vector modulus, the complex modulus and the general modulus, allow the computing of the modulus of scalar and vector quantities, expressed by real or complex numbers
Before describing the modulus functions, a recall of the notations is described in the following blocks.
Scalar quantities: notations
To define the modulus functions of the scalar quantities expressed by real and complex numbers, we use the following notations:
- for a real scalar : A
-
for a complex scalar : I
expressed by I = Ir + j Ii
where Ir and Ii are real scalars
Vector quantities: notations
To define the modulus functions of the vector quantities expressed by real and complex numbers, we use the following notations:
-
for a real vector : V
expressed by
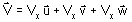
where Vx , Vy and Vz , are real scalars
-
for a complex vector : Vc
expressed by
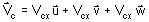
where Vcx , Vcy and Vcz are complex scalars
It is also possible to describe a complex vector in the form:
where Vxr , Vyr , Vzr , Vxi , Vyi and Vzi are real scalars.
Vector modulus: ModV function
The ModV (X) function returns the vector modulus of the X vector, which can be a real vector or a scalar vector.
- If V is a real vector, ModV(V) is a real scalar expressed by
- If V c is a complex vector, ModV(V c ) is a complex scalar expressed by:
Complex modulus: ModC function
The ModC (X) function returns the complex modulus of the complex argument X, which can be a complex scalar or a complex vector.
- If I is a complex scalar, ModC(I) is a real scalar expressed by:
- If Vc is a complex vector, ModC(Vc ) is a real vector expressed by:
General modulus: Mod function
The Mod (X) function returns the general modulus of the argument X. Whatever is type of the argument X (scalar or vector, real or complex), the result Mod(X) is a real scalar.
- If I is a complex scalar, Mod(I) is a real scalar expressed by:
- If V c is a complex vector, Mod(V c ) is a real scalar expressed by:
Overview
The results of the modulus functions (ModV, ModC and Mod) are described in the tables below.
|
Scalar quantity |
Vector modulus ModV | Complex modulus ModC | General modulus Mod |
|---|---|---|---|
|
real scalar A |
no interest | ||
|
complex scalar I = Ir + j Ii |
no interest not authorized |
real scalar
|
real scalar = |
| Vector quantity | Vector modulus ModV | Complex modulus ModC | General modulus Mod |
|---|---|---|---|
|
real vector V |
real scalar
|
no interest returns Vr |
real scalar = |
|
complex vector Vc = Vr + j Vi |
complex scalar = ModV (V r ) + j ModV (V i )
|
real vector
|
real scalar = ModV (ModC(Vc))
|