Steady State AC Magnetic: solved equations (introduction)
Introduction
The equations used for the solving are:
- Maxwell's equations (for a magnetic system)
- the constitutive equations of the matter
The computation conditions for a Steady state AC Magnetic application are the following:
- the state variables are time dependent: d/dt ≠ 0 (steady state sinusoidal: sinusoidal time dependence of the current sources)
-
the computation concerns only the B, H and E fields (the D field is not computed).
The equations of the electric fields E and D and of the magnetic fields B, H cannot be decoupled.
Equations and conditions
In the previously defined conditions of computation, the equations are summarized as follows:
|
E: electric
field strength (in V/m) B: magnetic flux density (in T) H: magnetic field strength (in A/m) J: current density (in A/m2) |
|||
|
σ : conductivity (in S) μ : permeability (in H/m) |
|||
The main equation for magnetic materials, can be put in form B(H) or H(B) as presented below.
|
|
⇒ |
|
μr : relative permeability μ0 : vacuum permeability |
|
|
⇒ |
|
νr : reluctivity νr =1/μr ν0 : vacuum reluctivity ν0 =1/μ0 |
Models
To solve these equations, two models are used:
-
the vector model, which uses: the magnetic vector potential (written
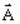 )
) -
the scalar model, which uses: magnetic scalar potentials (written ϕtot or ϕred)
Model and 2D or 3D application
The two models (vector and scalar) are proposed:- the vector model for the 2D applications
- the scalar model for the 3D applications