/VISC/PRONY

Format

Definition

Comments

1. For shell elements this model is available with /MAT/LAW66 and /MAT/LAW25 (COMPSH).

   For solid elements it is available with material laws /MAT/LAW38 (VISC_TAB), /MAT/LAW42 (OGDEN), /MAT/LAW69, /MAT/LAW70 (FOAM_TAB), /MAT/LAW82, /MAT/LAW88, /MAT/LAW90, /MAT/LAW92, /MAT/LAW103 (HENSEL-SPITTEL), and /MAT/LAW106 (JCOOK_ALM).

2. The viscosity effect is taken into account by using a Prony series. The deviatoric viscous stress is given by the convolution integral of the form:(1)
   $$S_{\mathit{ij}}={\displaystyle \underset{0}{\overset{t}{\int }}2G(t-s)\frac{\partial \mathit{dev}\left[{\epsilon }_{\mathit{ij}}\right]}{\partial s}}\mathit{ds}$$
   with(2)

   $$G(t)={\displaystyle \sum _{i=1}^M{G}_i{e}^{-{\beta }_{i}t}}$$

   and $\mathit{dev}\left[{\epsilon }_{\mathit{ij}}\right]$ denotes the deviatoric part of strain tensor.

   Shear decay:(3)

   $${\beta }_i=\left(\frac{1}{{\tau }_i}\right)$$

   Where, ${\tau }_i$ is the relaxation time.

3. For the viscous pressure, two formulations are available:
   • If the bulk relaxation modulus is $K_i>0$ , the viscous pressure is computed as:(4)
     $$P=-{\displaystyle {\int }_0^{t}K\left(s\right){\dot{\epsilon }}_{vol}}ds$$

     with ${\dot{\epsilon }}_{vol}=trace\left(\dot{\epsilon }\right)={\dot{\epsilon }}_{xx}+{\dot{\epsilon }}_{yy}+{\dot{\epsilon }}_{zz}$ and $K\left(t\right)={\displaystyle {\sum }_1^M{K}_i{e}^{-{\beta }_{ki}t}}$

   • If the bulk relaxation modulus is $K_i=0$ and the viscous bulk modulus $K_{\nu }>0$ , the viscous pressure is computed as:(5)
     $$P=-K_v{\dot{\epsilon }}_{vol}$$
4. Starting with Radioss version 2017, identical results are obtained using the same Prony coefficents G_i in /VISC/PRONY and viscoelastic materials /MAT/LAW34 (BOLTZMAN), /MAT/LAW40 (KELVINMAX), and /MAT/LAW42 (OGDEN). In previous Radioss versions, 2 G_i had to be input into /VISC/PRONY to get equivalent results.
5. Prony series parameters can be automatically fit from test data using the flag Itab:
   • If Itab = 1, prony series parameters are fitted from relaxation tests data, i.e moduli versus time curves.

     
     
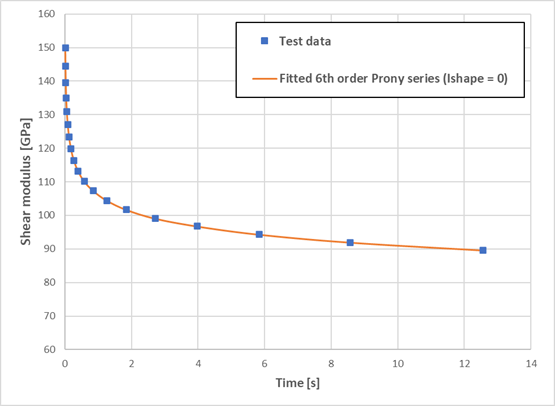
     Figure 1. Example of Prony series fitting on shear modulus relaxation test data

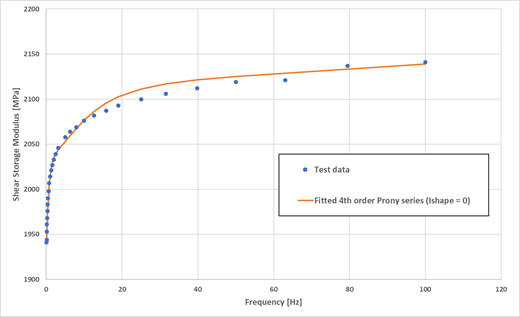
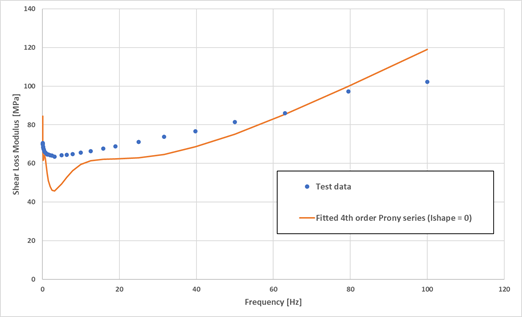
   • If Itab = 2, Prony series parameters are fitted from Dynamic Mechanical Analysis (DMA) tests data, i.e storage and loss moduli versus frequency curves.

     
     
     

     Figure 2. Example of Prony series fitting on shear storage and loss modulus DMA test data. data taken from [Tapia-Romero et al.,2020]

   In both cases, an automatic least-square fit is realized to find the parameters ( $G_i,{\beta }_i,K_i,{\beta }_{ki}$ ) in agreement with the order M of the Prony series defined by you. It is highly recommended to start with a small order and then increase it if the precision of the fitted curve is not sufficient.
   Note: The convergence of the least square fit may be hard to achieve for very high orders.
6. The shape of the fitted Prony series (only in case where Itab ≠ 0) can be chosen by you:
   • If Ishape = 0, the shape of the fitted Prony series are the same as the one given above, so as:(6)
     $$G(t)={\displaystyle \sum _{i=1}^M{G}_i{e}^{-{\beta }_{i}t}}$$
     and (7)

     $$K(t)={\displaystyle \sum _{i=1}^M{K}_i{e}^{-{\beta }_{ki}t}}$$
   • If Ishape = 1, the shape of the fitted Prony series is modified to consider the infinite values of the moduli, so as:(8)
     $$G(t)=G_{\infty }+{\displaystyle \sum _{i=1}^M{G}_i{e}^{-{\beta }_{i}t}}$$
     and(9)

     $$K(t)=K_{\infty }+{\displaystyle \sum _{i=1}^M{K}_i{e}^{-{\beta }_{ki}t}}$$
   Note: In this case, the infinite value of the moduli is taken as the last value of the relaxation test data curve if Itab = 1, or the first storage modulus value if Itab = 2.