Iron losses model

Introduction

In both cases, the defined model is only used for the computation in the post-processor. Iron losses are not taken into account in the solving process.

In Flux, the iron losses models are only available on the laminated regions, the magnetic flux density used in these models is the homogenized magnetic flux density in a block of iron sheets defined by:

${\mathit{B}}_{\mathit{h}}=K_f{\mathit{B}}_{\mathit{f}}+\left(1-K_f\right){\mathit{B}}_{\mathit{a}}$

In the presence of rotating magnetic fields the curve By = f (Bx) can have an elliptical shape, thus it is more judicious to decompose homogenized induction vector of induction homogenize as follows:

${\mathit{B}}_{\mathit{h}}=\left[\begin{array}{c}{B}_{\backslash \backslash }\\ B_{⏊}\end{array}\right]$

Those both axis correspond to the minor and major axes of the elliptical curve described by the Figure 1.

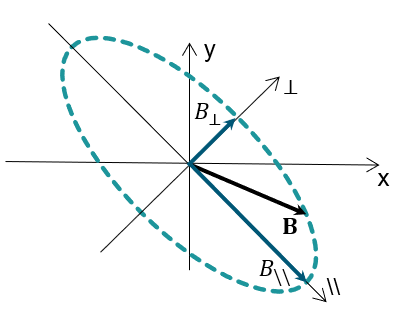
Figure 1. Curve By = f(Bx)

Modified Bertotti model

Presentation of the model:

The theory of Bertotti gives us the expression of the magnetic losses depending on the frequency and the magnetic flux density.

The power density is expressed with this transient magnetic relation:

$dP\left(t\right)=K_f\left(k_{1 }f{\left(\frac{∆B_{\backslash \backslash }+ ∆B_{⏊}}{K_f}\right)}^{{\alpha }_1}+k_{2 }g\left({\alpha }_2\right)\frac{1}{{K_f}^{{\alpha }_2}}{\left|\frac{d{B}_h}{dt}\right|}^{{\alpha }_2}+k_3 g\left({\alpha }_3\right)\frac{1}{{K_f}^{{\alpha }_3}}{\left|\frac{d{B}_h}{dt}\right|}^{{\alpha }_3}\right)$

$g\left({\alpha }_i\right)= \frac{2}{{\left(2\pi \right)}^{{\alpha }_i-1} 4\int {cos}^{{\alpha }_i}\left(\theta \right) d\theta }$

* the distinction between supplementary losses / in excess losses and classical losses is artificial. They can be grouped in one term and they therefore correspond to real induced currents flowing in the sheet.

An Excel sheet permitting to determine, coefficients and exponents (Modified Bertotti model identification tool) is available in the following path:

INSTALLATION_FOLDER\Flux\DocExamples\Tools\BertottiLossesCoefficients

in which INSTALLATION_FOLDER represents the Flux installation directory in your system.

To run the modified Bertotti model identification tool, open the file BertottiLossesCoefficients.xls available in that location in Microsoft Excel.

Limits of validity

In a Steady state AC Magnetic application, power density is expressed with the following equation:

$dP=\left(k_1 B_{max}^{{\alpha }_1} f+{k_2 {(B}_{max} f)}^{{\alpha }_2}+{k_3 {(B}_{max} f)}^{{\alpha }_3} \right)K_f$

The software use the value of the magnetic flux density in each point. Consequently, it is convenient to be very careful with the results concerning the problems represented by the rotating machines with the Steady state AC Magnetic simulation. Indeed, for this type of simulation the rotor has a fixed position with respect to the stator, and the real rotor movement is modeled by changing the resistivity of the conductors of the rotor electric circuit. Thus, the calculated magnetic flux density is maximum in a point on the given position of the rotor in relationship with the stator, due to space harmonics. It follows that the calculated magnetic flux density does not correspond to the peak value of the magnetic flux density over a period in the time domain if the rotor were turning. Consequently, the computation of the magnetic losses must be utilized in this case with much caution.

Moreover, in the case of a non-linear approximation for the magnetic behavior law B(H), the saturation phenomenon, introduced by means of an equivalent model of magnetization, can alter the local values of the magnetic flux density.

Steps of the modified Bertotti model definition in the material

LS model

Presentation:

Characteristic surface H(B, dB/dt):

For each of the materials, the characteristic surface H(B,dB/dt) can be obtained by using a Epstein type device for magnetic measurements in medium frequency.

An example of this type of surface is represented in the figure below.

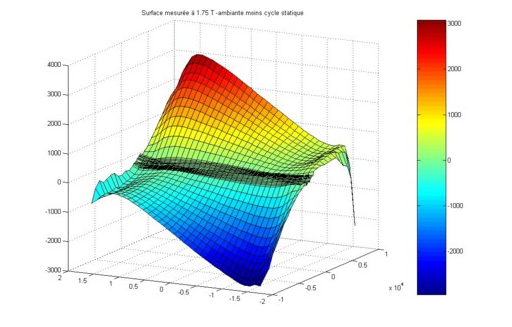
Figure 2. H(B, dB/dt) surface

Reconstruction of the cycle:

An analytical model permits the reconstruction of H field from values of B:

H(B,dB/dt) = Hstatic(B) +Hdynamic (B,dB/dt)

B(H) curves like those in the figure below can therefore be obtained, permitting the computations of iron losses quite accurately.

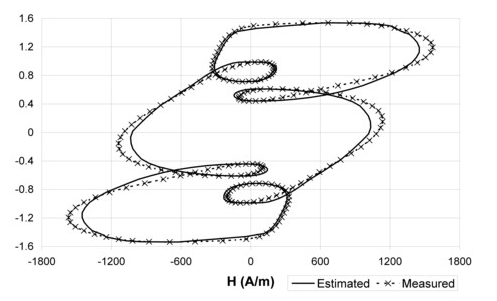
Figure 3. Sinusoidal magnetic flux density & 5th harmonic at 200Hz

The LS model is assigned to different nuances of laminations, which have been especially described to this purpose.

For more informations about electrical steel sheets, see this page: Standards for electrical steel sheets

With this model, the user can also import his own materials in Flux (see LS model identification with MILS).

Definiton of the LS model in the material

See the section below: Isotropic soft material : Iron sheets described by LS model