Turbulent Flow with Separation in an Asymmetric Diffuser

Problem Description

The problem consists of air flowing through an asymmetric diffuser with a divergent lower wall and a straight upper wall, as shown in the following image, which is not drawn to scale. The diffuser inlet has a height of 1.5 cm (H) and extends 9 cm (6H) to the divergent section. The lower wall of the diffuser diverges at an angle of 10° and expands to 7.05 cm (4.7H). The divergent section has a horizontal length of 31.5 cm (21H). The expanded section of the diffuser extends 84 cm (56H) to the outlet. Air, with a density of 1.225 kg/m³ and a viscosity of 1.8325 X 10^-5 kg/m-s enters the diffuser through the inlet of the diffuser with a fully developed turbulent profile at a Reynolds's number of 20,000. The simulation was conducted with the Reynolds Averaged Navier-Stokes equations using four turbulence models, Spalart Allmaras, Shear Stress Transport (SST), K-ω and Realizable K-ε.

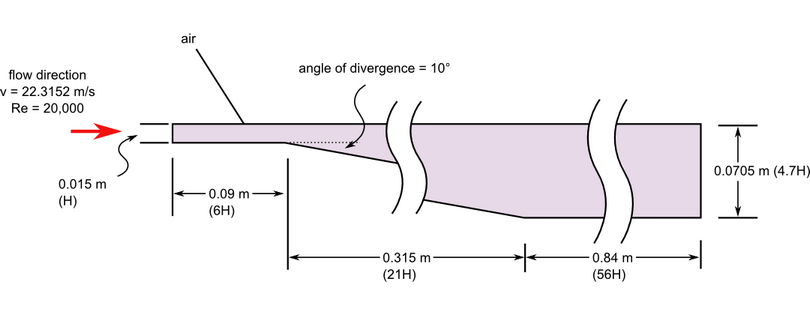
Figure 1. Critical Dimensions and Parameters for Simulating Turbulent Flow with Separation in an Asymmetric Diffuser

The simulation was performed as a two dimensional problem by constructing a volume mesh that contains a single layer of elements extruded in the cross stream direction (perpendicular to the flow plane) and by imposing symmetry boundary conditions on the extruded planes.

Figure 2. Mesh Details Near the Inlet and Divergent Section of Diffuser

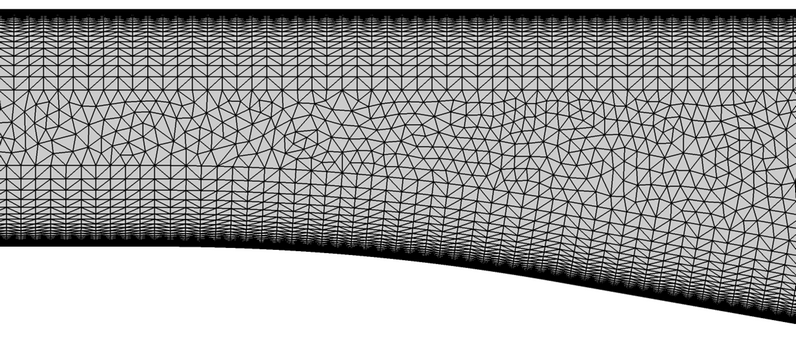
Figure 3. Mesh Details at the Beginning of the Divergence of the Lower Wall in the Diffuser

AcuSolve Results

The AcuSolve solution converged to a steady state and the results reflect the mean flow conditions. As the fully developed turbulent flow enters the divergent section, the peak velocity is maintained until the expansion of the cross-sectional height, forms an adverse pressure gradient. After the flow enters the divergent section, the velocity decreases significantly, due to the expansion of the cross-section height. This causes separation of the flow along the divergent wall and results in an area of recirculation. The bulk of the flow above the divergent wall maintains its streamwise direction, while a portion of it reverses direction before reattaching further downstream of the divergent section. The following images show the steady state flow solution for flow within the diffuser.

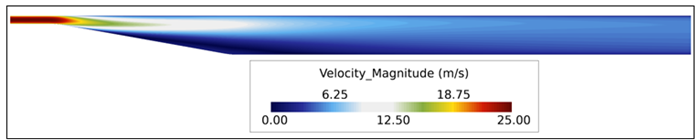
Figure 4. Velocity Contours Within the Diffuser

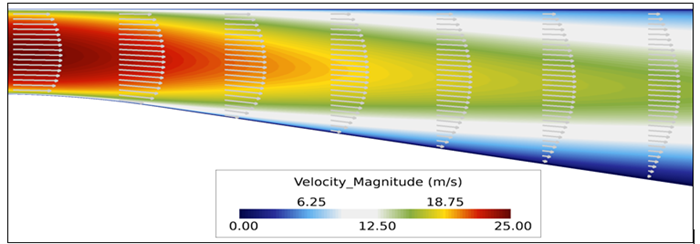
Figure 5. Close up View of Velocity Vectors and Contours of Velocity Magnitude in the Diffuser

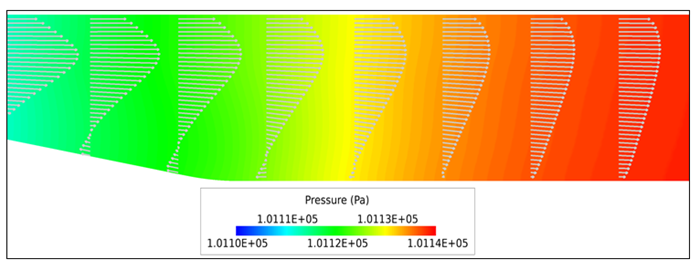
Figure 6. Close up View of Velocity Vectors and Contours of Pressure to Show Recirculation as it Approaches the Reattachment Point

Upstream of the diffuser section, the streamline velocity increases as the distance from the lower wall increases until it reaches the maximum velocity at the center of the channel. As the flow enters the divergent section of the channel, the streamwise velocity decreases near the bottom wall. The images below show the velocity profiles at three locations as measured from the midpoint of the curve where the bottom wall begins to diverge (X=0.0) for each of the tested turbulence models. The first location, where X/H = -5.944, is close to the inlet. The second location, where X/H = 13.468, is approximately 0.2 m downstream of the divergent section (~ 0.1 m from the fully expanded section). The third location, where X/H = 24.066, is approximately 0.16 m downstream of the point where the diffuser has reached the maximum height. In these plots the black circles represent the experimental measurements (Buice and Eaton 2000), the solid red lines for the prediction for the Spalart Allmaras model, solid blue lines for the prediction for the SST model, solid green lines for the prediction for the K-ω model and solid cyan lines for the K-ε model, representing the AcuSolve results. The non-dimensional height is represented by the fraction of the vertical height (Y) divided by the inlet height (H) and the velocity is normalized by the inlet velocity (Uref).

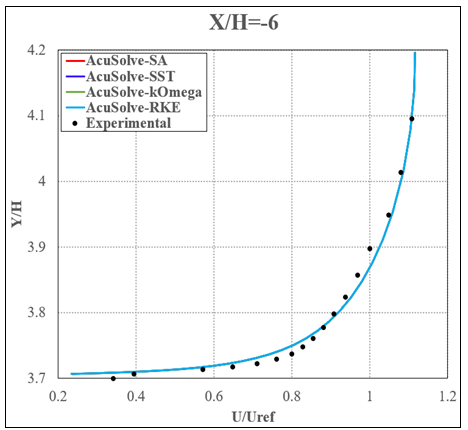
Figure 7. Non-Dimensional Streamwise Velocity Plotted Against Vertical Location Near the Inlet (X/H=-5.9442, Where the Reference Point is 6H Downstream of the Inlet)

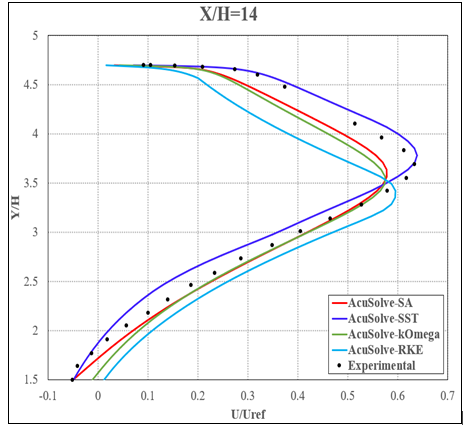
Figure 8. Non-Dimensional Streamwise Velocity Plotted Against Vertical Location Approximately 0.2 m Downstream of the Divergence (X/H = 13.468, Where the Reference Point is 6H Downstream of the Inlet)

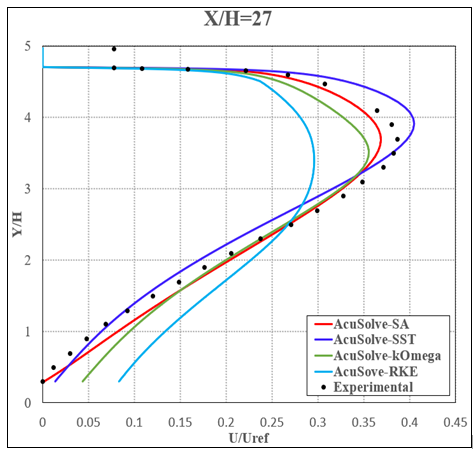
Figure 9. Non-Dimensional Streamwise Velocity Plotted Against Vertical Location Approximately 0.2 m Downstream of the Transition to the Fully Divergent Section (X/H = 27.066, Where the Reference Point is 6H Downstream of the Inlet)

The non-dimensional pressure coefficient (Cp), defined by the integrated inlet pressure and Uref predicted by AcuSolve along the bottom of the diffuser is compared to experimental results. The figure below shows Cp, along a constant vertical height, as a function of the streamwise distance from the inlet of the channel. The results demonstrate that AcuSolve is capable of accurately predicting the pressure within the diffuser within the expected range based on the type of turbulence model used. The performance of the three turbulence models were found to be consistent with previously published results for flow through the diffuser as published by Buice and Eaton (2000), with the SST model predicting the pressure distribution most accurately. Note that the inlet of the experimental duct was 6H longer than that modeled - AcuSolve values where X/H < -6 are reported as the inlet value.

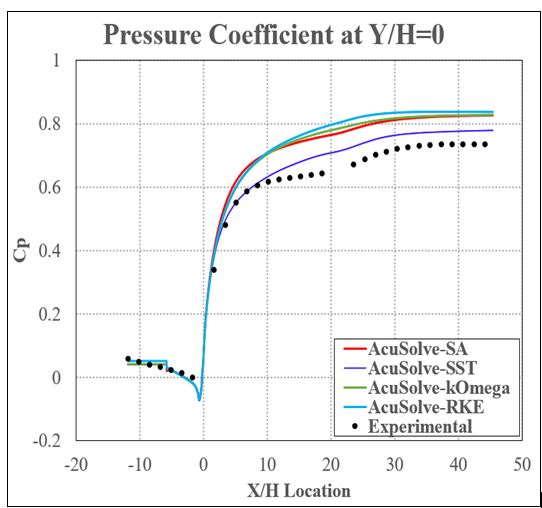
Figure 10. Non-Dimensional Pressure Coefficient (Cp) Plotted Against Relative Distance Along the Diffuser at a Constant Height Equal to the Bottom of the Inlet

Summary

In this application, a fully developed turbulent flow at a Reynolds number of 20,000 is studied. Due to the adverse pressure gradient, separation of flow occurs and causes recirculation in the divergent section of the diffuser. The results were found to be consistent with previously published computational studies and experimental data. The results of this validation demonstrate the ability of AcuSolve to accurately predict the separation point, the recirculation that occurs along the divergent wall, and the reattachment point in the straight section of the diffuser.

Simulation Settings for Turbulent Flow with Separation in an Asymmetric Diffuser

HyperWorks CFD database file: <your working directory>\asymmetric_diffuser_turbulent\asymmetric_diffuser_turbulent.hm

Global

• Problem Description
  • Analysis type - Steady State
  • Turbulence equation - Spalart Allmaras
• Auto Solution Strategy
  • Max time steps - 150
  • Relaxation Factor - 0.2
• Material Model
  • Air
    • Density - 1.225.0 kg/m3
    • Viscosity - 1.8325e-5 kg/m-sec

  Model

• Volume
  • Volume
    • Element Set
      • Material model - Air
• Surfaces
  • Bottom
    • Simple Boundary Condition
      • Type - Wall
  • Inlet
    • Simple Boundary Condition (disabled to allow for nodal boundary conditions to be set)
    • Advanced Options
      • Nodal Boundary Conditions
        • X-Velocity
          • Type - Linear
          • Precedence - 2
          • Curve fit variable - Y coordinate
          • Curve fit values (included in database)
        • Y-Velocity
          • Type - Linear
          • Precedence - 2
          • Curve fit variable - Y coordinate
          • Curve fit values (included in database)
        • Eddy Viscosity
          • Type - Linear
          • Precedence - 2
          • Curve fit variable - Y coordinate
          • Curve fit values (included in database)
  • Outlet
    • Simple Boundary Condition
      • Type - Outflow - 101139.0 Pa
  • Side 1
    • Simple Boundary Condition
      • Type - Symmetry
  • Side 2
    • Simple Boundary Condition
      • Type - Symmetry
  • Top
    • Simple Boundary Condition
      • Type - Wall

References

C.U. Buice, and J.K., Eaton. "Experimental Investigation of Flow Through an Asymmetric Plane Diffuser". Journal of Fluids Engineering 122:433-435. June 2000.

S. Obi, K. Aoki and S. Masuda. "Experimental and Computational Study of Turbulent Separating Flow in an Asymmetric Plane Diffuser". Ninth Symposium on Turbulent Shear Flows. p. 305. Kyoto, Japan. August 16-19, 1993.