Electro Static： 解を求める方程式

概要

Electro Staticアプリケーションで計算に使用する方程式は次のとおりです：

  • 電気システム向けの該当するMaxwellの方程式
  • 誘電材料の特性を記述する構成方程式

Electro Staticアプリケーションの計算条件は次のとおりです：

  • 計算はD界とE界を対象とし、B界とH界は計算されないこと。電界のDとEの方程式と磁界のBとHの方程式は非連成です。
  • 界が時間変化しないこと（静的であること、d/dt = 0）
  • 電流密度が0であること（J = 0）

方程式と条件

ここで定義した計算条件の下では、各方程式は次のようになります：

方程式 説明

E： 電界強度（V/m）

D： 電束密度（C/m2）

V： 電位（V）

q： 電荷密度（C/m3）

εr： 比誘電率

ε0： 真空の誘電率（F/m）

解を求める方程式

Electro Staticアプリケーションの場合、Fluxで有限要素法によって解く2次方程式は次のとおりです：

ここで：

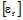  • ： 媒質の比導電率のテンソル
  • ε0： 真空の誘電率、ε0 = 1/(36π109)（F/m）
  • V： 電位（V）
  • q： 電荷密度（C/m3）

状態変数

Electro Staticアプリケーションの状態変数は電位V（Flux 3DではVeと記述します）です。

電位Vのスカラー場が一意であるためには、計算ドメインで1つまたは複数のポイントに、この電位の値を割り当てる必要があります。